题目内容
| |||||||||||||||
答案:
解析:
解析:
(1) |
解:设
|
(2) |
由题意 记 则
∴ ∴ ∴ |
(3) |
∴在数列
又 且 所以存在正整数 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
| |||||||||||||||
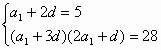 ………2分
………2分