题目内容
已知函数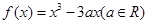
(1)当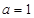 时,求
时,求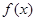 的极小值;
的极小值;
(2)若直线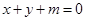 对任意的
对任意的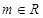 都不是曲线
都不是曲线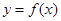 的切线,求
的切线,求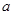 的取值范围;
的取值范围;
(3)设 ,求
,求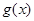 的最大值
的最大值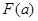 的解析式.
的解析式.
【答案】
(1)-2(2)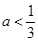 (3)
(3)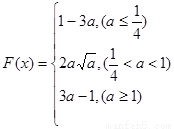
【解析】
试题分析:(1)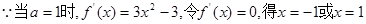 1分
1分
当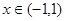 时,
时,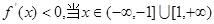 时,
时,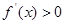 ,
,
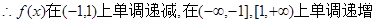 2分
2分
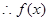 的极小值是
的极小值是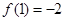 3分
3分
(2)法1: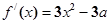 ,直线
,直线 即
即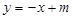 ,
,
依题意,切线斜率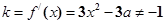 ,即
,即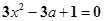 无解 4分
无解 4分
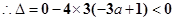
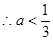 6分
6分
法2: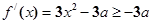 , 4分
, 4分
要使直线 对任意的
对任意的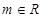 都不是曲线
都不是曲线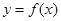 的切线,当且仅当
的切线,当且仅当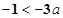 时成立,
时成立,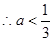 6分
6分
(3)因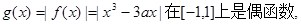
故只要求在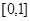 上的最大值.
7分
上的最大值.
7分
①当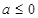 时,
时,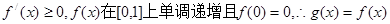
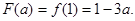 9分
9分
②当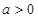 时,
时,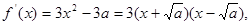
(ⅰ)当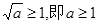

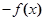 在
在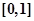 上单调递增,此时
上单调递增,此时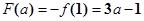 10分
10分
(ⅱ)当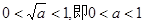 时,
时,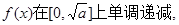 在
在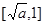 单调递增;
单调递增;
1°当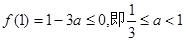 时,
时,
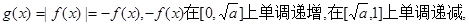
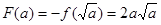 ;
;
2°当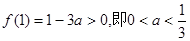
(ⅰ)当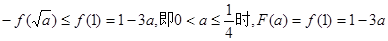
(ⅱ)当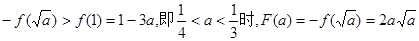
 13分
13分
综上 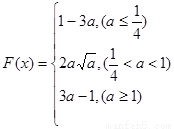 14分
14分
考点:导数的几何意义及函数极值最值
点评:利用函数在某一点处的导数值等于过改点的切线斜率可确定第二问中导数值不可能为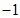 ,求函数极值最值首先求得导数,当导数等于0时得到极值点,确定单调区间从而确定是极大值还是极小值,第三问求最值要分情况讨论在区间
,求函数极值最值首先求得导数,当导数等于0时得到极值点,确定单调区间从而确定是极大值还是极小值,第三问求最值要分情况讨论在区间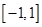 上的单调性,对于分情况讨论题是一个难点内容
上的单调性,对于分情况讨论题是一个难点内容

练习册系列答案
相关题目
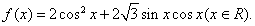
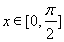
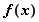

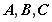
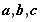
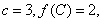
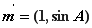
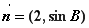
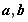

 时,求函数的最大值和最小值;
时,求函数的最大值和最小值; 的取值范围,使
的取值范围,使 在区间
在区间 上是单调减函数
上是单调减函数 .(
.( ).
). 时,求函数
时,求函数 的极值;
的极值; (2)若对
(2)若对 ,有成立,求实数
,有成立,求实数 的取值范围.
的取值范围.
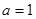 时,求
时,求 的极小值;
的极小值; ,求
,求 的最大值
的最大值 .
.