题目内容
已知{an}是正数组成的数列,a1=1,且点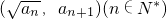 在函数y=x2+1的图象上.数列{bn}满足b1=0,bn+1=bn+3an(n∈N*).
在函数y=x2+1的图象上.数列{bn}满足b1=0,bn+1=bn+3an(n∈N*).
(I)求数列{an},{bn}的通项公式;
(II)若cn=anbncosnπ(n∈N*),求数列{cn}的前n项和Sn.
解:(Ⅰ)因为点( 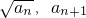 )(n∈N*)在函数y=x2+1的图象上
)(n∈N*)在函数y=x2+1的图象上
所以an+1=an+1
根据等差数列的定义:{an}是首项为1,公差为1的等差数列
所以an=n
∵bn+1=bn+3an(n∈N*).
∴bn+1-bn=3n(n∈N*).
∴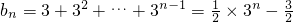
(II)∵cn=anbncosnπ(n∈N*),
∴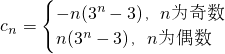
当n为偶数时,Sn=(-3+2•32+…+n•3n)+3[1-2+3-4+…+(n-1)-n]
设Tn=(-3+2•32+…+n•3n),则3Tn=-32+2•33+…+n•3n+1
∴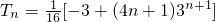
∴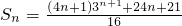
当n为奇数时,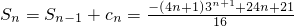
∴
分析:(Ⅰ)由题设条件知an+1=an+1,根据等差数列的定义:{an}是首项为1,公差为1的等差数列,从而an=n,根据bn+1=bn+3an(n∈N*),可得bn+1-bn=3n(n∈N*).累加可求和,从而得{bn}的通项公式;
(II)根据cn=anbncosnπ(n∈N*),可得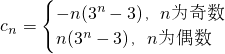 ,再分n为偶数,奇数分别求和即可
,再分n为偶数,奇数分别求和即可
点评:本题以函数为载体,考查数列的概念和性质及其应用,,考查错位相减法求和,解题时要注意公式的灵活运用.
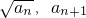 )(n∈N*)在函数y=x2+1的图象上
)(n∈N*)在函数y=x2+1的图象上所以an+1=an+1
根据等差数列的定义:{an}是首项为1,公差为1的等差数列
所以an=n
∵bn+1=bn+3an(n∈N*).
∴bn+1-bn=3n(n∈N*).
∴
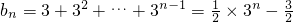
(II)∵cn=anbncosnπ(n∈N*),
∴
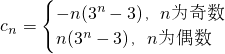
当n为偶数时,Sn=(-3+2•32+…+n•3n)+3[1-2+3-4+…+(n-1)-n]
设Tn=(-3+2•32+…+n•3n),则3Tn=-32+2•33+…+n•3n+1
∴
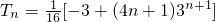
∴
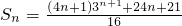
当n为奇数时,
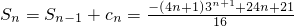
∴

分析:(Ⅰ)由题设条件知an+1=an+1,根据等差数列的定义:{an}是首项为1,公差为1的等差数列,从而an=n,根据bn+1=bn+3an(n∈N*),可得bn+1-bn=3n(n∈N*).累加可求和,从而得{bn}的通项公式;
(II)根据cn=anbncosnπ(n∈N*),可得
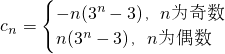 ,再分n为偶数,奇数分别求和即可
,再分n为偶数,奇数分别求和即可点评:本题以函数为载体,考查数列的概念和性质及其应用,,考查错位相减法求和,解题时要注意公式的灵活运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
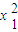 +
+ +…+
+…+ ,B=x1x2+x2x3+…+xn-1xn+xnx1其中x1,x2,…xn都是正数,则A≤B;
,B=x1x2+x2x3+…+xn-1xn+xnx1其中x1,x2,…xn都是正数,则A≤B; +
+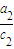 +
+ 的最小值为3;
的最小值为3; +
+ +…+
+…+ +
+ 的最小值为
的最小值为 .
.