题目内容
已知关于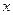 的不等式
的不等式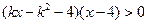 ,其中
,其中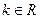 。
。
⑴试求不等式的解集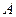 ;
;
⑵对于不等式的解集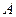 ,若满足
,若满足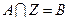 (其中
(其中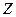 为整数集)。试探究集合
为整数集)。试探究集合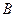 能否为有限集?若能,求出使得集合
能否为有限集?若能,求出使得集合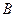 中元素个数最少的
中元素个数最少的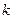 的所有取值,并用列举法表示集合
的所有取值,并用列举法表示集合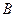 ;若不能,请说明理由。
;若不能,请说明理由。
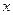 的不等式
的不等式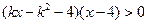 ,其中
,其中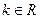 。
。⑴试求不等式的解集
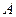 ;
;⑵对于不等式的解集
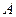 ,若满足
,若满足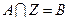 (其中
(其中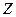 为整数集)。试探究集合
为整数集)。试探究集合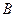 能否为有限集?若能,求出使得集合
能否为有限集?若能,求出使得集合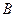 中元素个数最少的
中元素个数最少的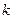 的所有取值,并用列举法表示集合
的所有取值,并用列举法表示集合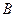 ;若不能,请说明理由。
;若不能,请说明理由。(1)见解析(2)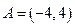 ,故集合
,故集合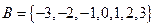
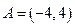 ,故集合
,故集合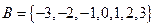
(1)当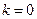 时,
时,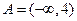 ;当
;当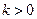 且
且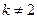 时,
时,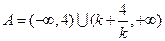 ;
;
当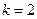 时,
时,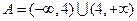 ;(不单独分析
;(不单独分析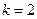 时的情况不扣分)
时的情况不扣分)
当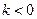 时,
时,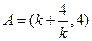 。(10分)
。(10分)
(2)由(1)知:当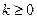 时,集合
时,集合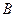 中的元素的个数无限;
中的元素的个数无限;
当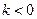 时,集合
时,集合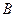 中的元素的个数有限,此时集合
中的元素的个数有限,此时集合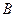 为有限集。(12分)
为有限集。(12分)
因为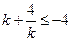 ,当且仅当
,当且仅当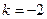 时取等号,
时取等号,
所以当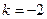 时,集合
时,集合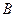 的元素个数最少。(14分)
的元素个数最少。(14分)
此时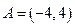 ,故集合
,故集合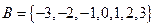 。(16分)
。(16分)
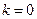 时,
时,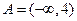 ;当
;当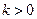 且
且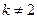 时,
时,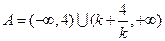 ;
;当
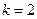 时,
时,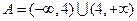 ;(不单独分析
;(不单独分析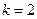 时的情况不扣分)
时的情况不扣分)当
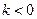 时,
时,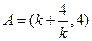 。(10分)
。(10分)(2)由(1)知:当
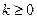 时,集合
时,集合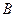 中的元素的个数无限;
中的元素的个数无限;当
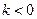 时,集合
时,集合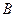 中的元素的个数有限,此时集合
中的元素的个数有限,此时集合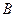 为有限集。(12分)
为有限集。(12分)因为
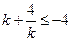 ,当且仅当
,当且仅当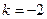 时取等号,
时取等号,所以当
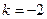 时,集合
时,集合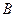 的元素个数最少。(14分)
的元素个数最少。(14分)此时
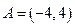 ,故集合
,故集合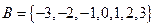 。(16分)
。(16分)
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
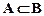 B.
B. 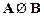 C.
C. 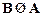 D. A∩B=
D. A∩B=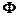
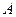 是由适合以下性质的函数组成:对于任意
是由适合以下性质的函数组成:对于任意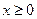 ,
,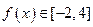 ,且
,且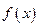 在
在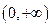 上是增函数,
上是增函数,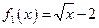 及
及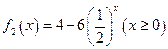 是否在集合
是否在集合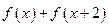
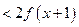 是否对任意
是否对任意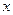
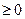 恒成立,试证明你的结论.
恒成立,试证明你的结论.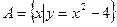 ,
,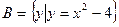 ,
,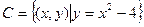 之间的关系
之间的关系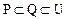 ,若令P、Q的一个集合运算表达式,使运算结果为空集,则这个运算表达式可以是______________。(只需写出一个表达式)
,若令P、Q的一个集合运算表达式,使运算结果为空集,则这个运算表达式可以是______________。(只需写出一个表达式)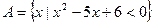 ,函数
,函数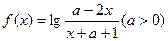 的定义域为集合
的定义域为集合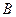 ,且
,且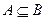 ,求实数
,求实数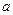 的取值范围。
的取值范围。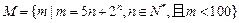 ,则集合M中所有元素的和为 ▲ .
,则集合M中所有元素的和为 ▲ .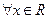 ,
,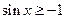 ”的否定是 .
”的否定是 .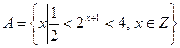 的元素个数有 个.
的元素个数有 个.