某学校为调查高三年级的240名学生完成课后作业所需时间.采取了两种抽样调查的方式:第一种由学生会的同学随机抽取24名同学进行调查,第二种由教务处对高三年级的学生进行编号.从001到240.抽取学号最后一位为3的同学进行调查.则这两种抽样方法依次为 A．分层抽样.简单随机抽样 B．简单随机抽样.分层抽样 C．分层抽样.系统抽样 D．简单随机抽样.系统抽样题目和参考答案——青夏教育精英家教网—

题目内容

某学校为调查高三年级的240名学生完成课后作业所需时间，采取了两种抽样调查的方式：第一种由学生会的同学随机抽取24名同学进行调查；第二种由教务处对高三年级的学生进行编号，从001到240，抽取学号最后一位为3的同学进行调查，则这两种抽样方法依次为 ( )

A．分层抽样，简单随机抽样	B．简单随机抽样，分层抽样
C．分层抽样，系统抽样	D．简单随机抽样，系统抽样

解析试题分析：第一种强调的是随机抽取故属于简单随机抽样；第二种强调抽取的是学号最后一位为3的同学，属系统抽样。故D正确。
考点：统计中的抽样方法。

练习册系列答案

相关题目

在一次实验中，测得的四组值分别是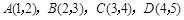，则与之间的回归直线方程为（）

为了解某地区的中小学生的课业负担情况，拟从该地区的中小学生中抽取部分学生进行调查，事先已了解到该地区小学、初中、高中三个学段学生的课业负担情况有较大差异，而男女生课业负担差异不大。在下面的抽样方法中，最合理的抽样方法是( )

2014年3月，为了调查教师对第十二届全国人民代表大会二次会议的了解程度，安庆市拟采用分层抽样的方法从三所不同的中学抽取60名教师进行调查.已知学校中分别有180，270，90名教师，则从学校中应抽取的人数为（）.

从某项综合能力测试中抽取100人的成绩，统计如表，则这100人成绩的标准差为（）

分数	5	4	3	2	1
人数	20	10	30	30	10

B．3 C．

D．

下表是某旅游区游客数量与平均气温的对比表：

平均气温(℃)	－1	4	10	13	18	26
数量(百个)	20	24	34	38	50	64

若已知游客数量与平均气温是线性相关的，则回归方程为（）．
A.

一次选拔运动中，测得7名选手的身高(单位：cm)分布茎叶图如图，

记录的平均身高为177cm，有一名候选人的身高记录不清楚，其末位数记为x，那么x的值为( )

登山族为了了解某山高y（km）与气温x（°C）之间的关系，随机统计了4次山高与相应的气温，并制作了对照表：

气温x（°C）	18	13	10	-1
山高y（km）	24	34	38	64

由表中数据，得到线性回归方程

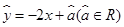，由此请估计出山高为72（km）处气温的度数为（）
A.-10 B.-8 C.-6 D.-6

变量X与Y相对应的一组数据为(10,1),(11.3,2),
(11.8,3),(12.5,4),(13,5),变量U与V相对应的一组数据为(10,5),(11.3,4),
(11.8,3),(12.5,2),(13,1).r₁表示变量Y与X之间的线性相关系数,r₂表示变量V与U之间的线性相关系数,则(　　)

A．r₂<r₁<0	B．0<r₂<r₁
C．r₂<0<r₁	D．r₂=r₁

试题分类