题目内容
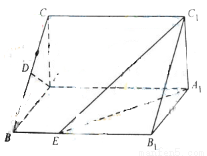
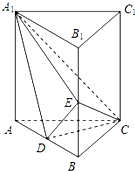 如图,直棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点,AA1=AC=CB=
如图,直棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点,AA1=AC=CB=
| ||
| 2 |
(1)证明:DC⊥DE;
(2)求EC与平面A1DC所成角的正弦值.
分析:(1)证明CD⊥AB,CD⊥AA1,可得CD⊥面A1ABB1,从而可得DC⊥DE;
(2)证明DE⊥面A1DC,可得所求角的平面角为∠ECD,从而可求EC与平面A1DC所成角的正弦值.
(2)证明DE⊥面A1DC,可得所求角的平面角为∠ECD,从而可求EC与平面A1DC所成角的正弦值.
解答:(1)证明:由AC=CB=
AB,知CD⊥AB,
又直棱柱ABC-A1B1C1中,D分别是AB的中点,
所以CD⊥AA1,
因为AA1∩AB=A,
所以CD⊥面A1ABB1,
因为DE?面A1ABB1,
所以DC⊥DE;
(2)解:设AA1=2a,则可得A1D=
a,DE=
a,A1E=3a,
所以A1E2=A1D2+DE2,
故A1D⊥DE,
又由(1)得DC⊥DE,A1D∩DC=D,
所以DE⊥面A1DC,故所求角的平面角为∠ECD,
故sin∠ECD=
=
=
.
| ||
| 2 |
又直棱柱ABC-A1B1C1中,D分别是AB的中点,
所以CD⊥AA1,
因为AA1∩AB=A,
所以CD⊥面A1ABB1,
因为DE?面A1ABB1,
所以DC⊥DE;
(2)解:设AA1=2a,则可得A1D=
| 6 |
| 3 |
所以A1E2=A1D2+DE2,
故A1D⊥DE,
又由(1)得DC⊥DE,A1D∩DC=D,
所以DE⊥面A1DC,故所求角的平面角为∠ECD,
故sin∠ECD=
| DE |
| CE |
| ||
|
| ||
| 5 |
点评:本题考查线面垂直的判定与性质,考查线面角,正确运用线面垂直的判定定理是关键.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
 如图,直棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点,AA1=AC=CB=
如图,直棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点,AA1=AC=CB=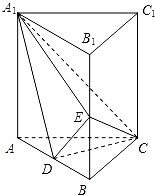 如图,直棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点,
如图,直棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点,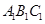 中,D,E分别是AB,BB1的中点,
中,D,E分别是AB,BB1的中点,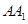 =AC=CB=
=AC=CB=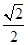 AB.
AB.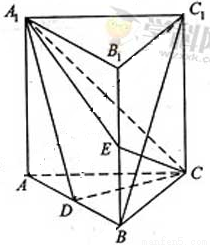
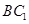 //平面
//平面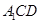 ;
;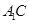 -E的正弦值.
-E的正弦值. ,AA1=3,D是BC的中点,点E在菱BB1上运动。
,AA1=3,D是BC的中点,点E在菱BB1上运动。