题目内容
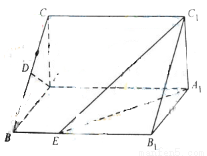
 如图,直棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点,AA1=AC=CB=
如图,直棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点,AA1=AC=CB=
| ||
| 2 |
(1)证明:DC⊥DE;
(2)求三棱锥C-A1DE的体积.
分析:(1)由韦达定理可得△ABC为等腰直角三角形,进而可得CD⊥AB,结合直棱柱的特征可得CD⊥AA1,结合线面垂直的判定定理可得CD⊥面A1ABB1,进而由线面垂直的定义可得DC⊥DE;
(2)由(1)可得CD⊥面A1ABB1,即CD为棱锥的高,求出三角形△A1DE的面积后,代入棱锥的体积公式,可得三棱锥C-A1DE的体积.
(2)由(1)可得CD⊥面A1ABB1,即CD为棱锥的高,求出三角形△A1DE的面积后,代入棱锥的体积公式,可得三棱锥C-A1DE的体积.
解答:证明:(1)由AC=CB=
AB,
AC2+CB2=AB2
故△ABC为等腰直角三角形
又由D是AB的中点,
知CD⊥AB,
又∵直棱柱ABC-A1B1C1中,AA1⊥平面ABC,CD?平面ABC,
∴CD⊥AA1,
又∵AB,AA1?面A1ABB1,AB∩AA1=A
∴CD⊥面A1ABB1,
又∵DE?面A1ABB1,
故DC⊥DE;
(2)由(1)知CD⊥面A1ABB1,且CD=
在Rt△A1AD中,AA1=2,AD=
,
故A1D=
在Rt△BDE中,BE=1,BD=
,
故DE=
Rt△A1B1E中,A1B1=2
,B1E=1
故A1E=3
∵A1E2=A1D2+DE2
故三角形△A1DE为直角三角形
故VC-A1DE=
•CD•
•A1D•DE=
•
•
•
•
=1.
| ||
| 2 |
AC2+CB2=AB2
故△ABC为等腰直角三角形
又由D是AB的中点,
知CD⊥AB,
又∵直棱柱ABC-A1B1C1中,AA1⊥平面ABC,CD?平面ABC,
∴CD⊥AA1,
又∵AB,AA1?面A1ABB1,AB∩AA1=A
∴CD⊥面A1ABB1,
又∵DE?面A1ABB1,
故DC⊥DE;
(2)由(1)知CD⊥面A1ABB1,且CD=
| 2 |
在Rt△A1AD中,AA1=2,AD=
| 2 |
故A1D=
| 6 |
在Rt△BDE中,BE=1,BD=
| 2 |
故DE=
| 3 |
Rt△A1B1E中,A1B1=2
| 2 |
故A1E=3
∵A1E2=A1D2+DE2
故三角形△A1DE为直角三角形
故VC-A1DE=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 2 |
| 1 |
| 2 |
| 6 |
| 3 |
点评:本题考查的知识点是线面垂直的判定定理及性质,棱锥的体积,其中证明出直线CD⊥面A1ABB1,是解答的关键.

练习册系列答案
 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
 如图,直棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点,AA1=AC=CB=
如图,直棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点,AA1=AC=CB= 如图,直棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点,AA1=AC=CB=
如图,直棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点,AA1=AC=CB= 中,D,E分别是AB,BB1的中点,
中,D,E分别是AB,BB1的中点,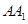 =AC=CB=
=AC=CB=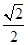 AB.
AB.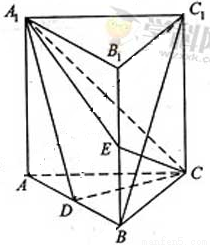
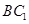 //平面
//平面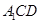 ;
;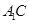 -E的正弦值.
-E的正弦值. ,AA1=3,D是BC的中点,点E在菱BB1上运动。
,AA1=3,D是BC的中点,点E在菱BB1上运动。