题目内容
已知平面上的线段l及点P,在l上任取一点Q,线段PQ长度的最小值称为点P到线段l的距离,记作d(P,l).(1)已知P(1,1),线段l:x-y-3=0(3≤x≤5),求d(P,l);
(2)设A(-1,0),B(1,0),求点集D={P|d(P,AB)≤1}所表示图形的面积;
(3)若M(0,1),O(0,0),N(2,0),画出集合Ω={P|d(P,MO)=d(P,NO)}所表示的图形.
【答案】分析:(1)根据d(P,l)的定义,结合两点间的距离公式和二次函数的性质,即可算出的值d(P,l).
(2)d(P,AB)≤1,即Q在线段AB上时线段PQ长度的最小值不超过1,由此结合点A、B的坐标,利用距离公式即可化简出所求图形的边界曲线方程,结合矩形面积与圆面积公式可得该图形的面积;
(3)算出MO、NO的方程,利用题中P到线段l的距离的定义,建立关系式并化简整理,可得集合Ω表示的曲线方程,再根据曲线方程作出相应的图形,可得答案.
解答:解:(1)设Q(x,x-3)是线段l:x-y-3=0(3≤x≤5)上一点,则
|PQ|=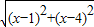 =
=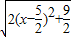 ,(3≤x≤5)…(3分)
,(3≤x≤5)…(3分)
当x=3时,d(P,l)=|PQ|最小值= . …(4分)
. …(4分)
(2)点集D由如下曲线围成
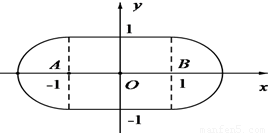
l1:y=1(|x|≤1),l2:y=-1(|x|≤1),
C1:(x+1)2+y2=1(x≤-1),C2:(x-1)2+y2=1(x≥1),
其面积为S=4+π. …(8分)
(3)根据题意,可得
线段MO、NO的方程分别为x=0(0≤y≤1)、y=0(0≤x≤2),
∴Ω={(x,y)|x≤0,y≤0}∪{(x,y)|y=x,0<x≤1}∪{(x,y)|x2=2y-1,1<x≤2}
∪{(x,y)|4x-2y-3=0,x>2}…(12分)
其所表示的图形为右图中的阴影区域(含x,y轴负半轴)及曲线OABC.…(14分)
点评:本题给出点P到线段l的距离的定义,求实际问题中的距离并讨论相应的曲线方程.着重考查了点到直线的距离公式、二次函数的性质和曲线与方程的化简等知识,属于中档题.
(2)d(P,AB)≤1,即Q在线段AB上时线段PQ长度的最小值不超过1,由此结合点A、B的坐标,利用距离公式即可化简出所求图形的边界曲线方程,结合矩形面积与圆面积公式可得该图形的面积;
(3)算出MO、NO的方程,利用题中P到线段l的距离的定义,建立关系式并化简整理,可得集合Ω表示的曲线方程,再根据曲线方程作出相应的图形,可得答案.
解答:解:(1)设Q(x,x-3)是线段l:x-y-3=0(3≤x≤5)上一点,则
|PQ|=
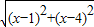 =
=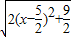 ,(3≤x≤5)…(3分)
,(3≤x≤5)…(3分)当x=3时,d(P,l)=|PQ|最小值=
 . …(4分)
. …(4分)(2)点集D由如下曲线围成


l1:y=1(|x|≤1),l2:y=-1(|x|≤1),
C1:(x+1)2+y2=1(x≤-1),C2:(x-1)2+y2=1(x≥1),
其面积为S=4+π. …(8分)
(3)根据题意,可得
线段MO、NO的方程分别为x=0(0≤y≤1)、y=0(0≤x≤2),
∴Ω={(x,y)|x≤0,y≤0}∪{(x,y)|y=x,0<x≤1}∪{(x,y)|x2=2y-1,1<x≤2}
∪{(x,y)|4x-2y-3=0,x>2}…(12分)
其所表示的图形为右图中的阴影区域(含x,y轴负半轴)及曲线OABC.…(14分)
点评:本题给出点P到线段l的距离的定义,求实际问题中的距离并讨论相应的曲线方程.着重考查了点到直线的距离公式、二次函数的性质和曲线与方程的化简等知识,属于中档题.

练习册系列答案
相关题目
 。
。 ,线段
,线段 ,求
,求 所表示图形的面积;
所表示图形的面积; 所表示的图形。(本题满分14分)
所表示的图形。(本题满分14分)