题目内容
有人从“若a<b,则2a<
<2b”中找到灵感引入一个新概念,设F(x)=x2,f(x)=2x,于是有f(a)<
<f(b),此时称F(x)为甲函数,f(x)为乙函数,下面命题正确的是( )
| b2-a2 |
| b-a |
| F(b)-F(a) |
| b-a |
分析:根据引入的新概念,可知y=f(x)是R上的增函数,由于A,B,C中的函数不是R上的单调函数,故可排除,对于D,利用条件,即可验证.
解答:解:由题意,∵a<b,f(a)<
<f(b),
∴y=f(x)是R上的增函数,从而A,B,C不正确
对于D,f(x)=ex,则e2<
<e3,e3<
<e5
∴F(3)-F(2)>0,F(5)-F(3)>0
∴F(5)>F(3)>F(2)
故D正确.
故选D.
| F(b)-F(a) |
| b-a |
∴y=f(x)是R上的增函数,从而A,B,C不正确
对于D,f(x)=ex,则e2<
| F(3)-F(2) |
| 3-2 |
| F(5)-F(3) |
| 5-3 |
∴F(3)-F(2)>0,F(5)-F(3)>0
∴F(5)>F(3)>F(2)
故D正确.
故选D.
点评:本题以新定义为素材,考查学生对新定义的理解,考查新定义的运用,正确理解新定义是解题的前提

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
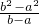 <2b”中找到灵感引入一个新概念,设F(x)=x2,f(x)=2x,于是有f(a)<
<2b”中找到灵感引入一个新概念,设F(x)=x2,f(x)=2x,于是有f(a)<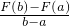 <f(b),此时称F(x)为甲函数,f(x)为乙函数,下面命题正确的是
<f(b),此时称F(x)为甲函数,f(x)为乙函数,下面命题正确的是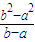 <2b”中找到灵感引入一个新概念,设F(x)=x2,f(x)=2x,于是有f(a)<
<2b”中找到灵感引入一个新概念,设F(x)=x2,f(x)=2x,于是有f(a)<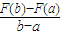 <f(b),此时称F(x)为甲函数,f(x)为乙函数,下面命题正确的是( )
<f(b),此时称F(x)为甲函数,f(x)为乙函数,下面命题正确的是( )