题目内容
已知椭圆的中心在原点,焦点在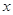 轴上,一个顶点为
轴上,一个顶点为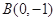 ,且其右焦点到直线
,且其右焦点到直线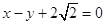 的距离为3.
的距离为3.
(Ⅰ)求椭圆方程;
(Ⅱ)设直线过定点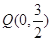 ,与椭圆交于两个不同的点
,与椭圆交于两个不同的点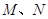 ,且满足
,且满足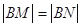 .
.
求直线的方程.
【答案】
(1)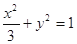
(2))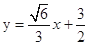 或
或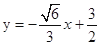 .
.
【解析】
试题分析:(1)设椭圆方程为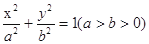 , 则
, 则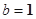 .
1分
.
1分
令右焦点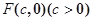 , 则由条件得
, 则由条件得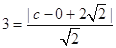 ,得
,得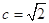 3分
3分
那么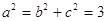 ,∴椭圆方程为
,∴椭圆方程为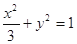 . 4分
. 4分
(2)若直线斜率不存在时,直线即为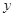 轴,此时
轴,此时 为椭圆的上下顶点,
为椭圆的上下顶点,
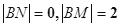 ,不满足条件; 5分
,不满足条件; 5分
故可设直线: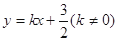 ,与椭圆
,与椭圆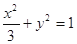 联立,
联立,
消去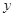 得:
得: 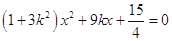 . 6分
. 6分
由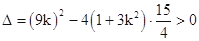 ,得
,得 .
7分
.
7分
由韦达定理得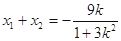
而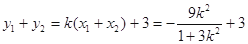 8分
8分
设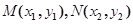 的中点
的中点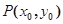 ,则
,则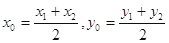
由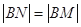 ,则有
,则有 .
.
 10分
10分
可求得 . 11分
. 11分
检验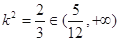 12分
12分
所以直线方程为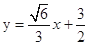 或
或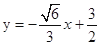 .
3分
.
3分
考点:直线与椭圆的位置关系
点评:主要是考查了直线与椭圆的位置关系的运用,属于基础题。

练习册系列答案
相关题目