题目内容
1. 已知平面直角坐标系中的一个椭圆,它的中心在原点,左焦点为F(-$\sqrt{3}$,0),且抛物线x2=4y的焦点为椭圆的一个顶点,过P(0,2)的直线l分别与椭圆,抛物线交于不同的A,B,C,D四点.
已知平面直角坐标系中的一个椭圆,它的中心在原点,左焦点为F(-$\sqrt{3}$,0),且抛物线x2=4y的焦点为椭圆的一个顶点,过P(0,2)的直线l分别与椭圆,抛物线交于不同的A,B,C,D四点.(Ⅰ)求该椭圆的标准方程
(Ⅱ)求证:∠COD为钝角(其中O为坐标原点);
(Ⅲ)设点A,B的横坐标分别为s,t求|s-t|取最大值时直线l的方程.
分析 (I)依题意设椭圆的方程为:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$,利用抛物线x2=4y的焦点坐标为(0,1),可得b=1,又$c=\sqrt{3}$,可得a=2,即可求出椭圆的方程;
(Ⅱ)设直线l的方程为:y=kx+2,代入x2=4y,利用韦达定理,结合数量积公式,即可证明;
(Ⅲ)y=kx+2代入$\frac{x^2}{4}+{y^2}=1$,利用韦达定理,求出|s-t|,利用基本不等式求最值,即可得出结论.
解答 (I)解:依题意设椭圆的方程为:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$,
∵抛物线x2=4y的焦点坐标为(0,1),
∴b=1,
又$c=\sqrt{3}$,∴a=2,
∴椭圆的方程为$\frac{x^2}{4}+{y^2}=1$;
(Ⅱ)证明:设直线l的方程为:y=kx+2,
代入x2=4y,可得x2-4kx-8=0,
设C(x1,y1),D(x2,y2),则x1x2=-8,y1y2=4,
∴cos∠COD=x1x2+y1y2=-4<0,
∴∠COD为钝角(其中O为坐标原点);
(Ⅲ)解:y=kx+2代入$\frac{x^2}{4}+{y^2}=1$,可得(4k2+1)x2+16kx+12=0,
∴△=64k2-48>0,
∴k2>$\frac{3}{4}$,
∵点A,B的横坐标分别为s,t,
∴s+t=-$\frac{16k}{4{k}^{2}+1}$,st=$\frac{12}{4{k}^{2}+1}$,
∴(s-t)2=(-$\frac{16k}{4{k}^{2}+1}$)2-4×$\frac{12}{4{k}^{2}+1}$=$\frac{16(4{k}^{2}-3)}{(4{k}^{2}+1)^{2}}$,
设m=$\sqrt{4{k}^{2}-3}$>0,则k2=$\frac{{m}^{2}+3}{4}$,
∴|s-t|=$\frac{4m}{{m}^{2}+4}$=$\frac{4}{m+\frac{4}{m}}$≤$\frac{4}{2\sqrt{m•\frac{4}{m}}}$=1,当且仅当m=2时等号成立,
∴m=$\sqrt{4{k}^{2}-3}$=2,
∴k=±$\frac{\sqrt{7}}{2}$,
∴k=±$\frac{\sqrt{7}}{2}$时,|s-t|取最大值,直线l的方程为y=±$\frac{\sqrt{7}}{2}$x+2.
点评 本题考查椭圆方程,考查直线与椭圆的位置关系,考查韦达定理的运用,正确运用韦达定理是关键.

 名校课堂系列答案
名校课堂系列答案| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | 2 |

| A. | 0 | B. | $\frac{\sqrt{2}}{2}$+1 | C. | $\sqrt{2}$+1 | D. | $\frac{\sqrt{2}}{2}$ |
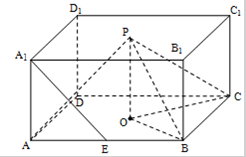 如图,P、O分别是正四棱柱ABCD-A1B1C1D1上、下底中心,E是AB的中点,AB=kAA1=2$\sqrt{2}$.
如图,P、O分别是正四棱柱ABCD-A1B1C1D1上、下底中心,E是AB的中点,AB=kAA1=2$\sqrt{2}$. 矩形ABCD所在平面垂直于三角形ABE所在平面,AB=2AE=3,AD=2,∠ABE=30°,点F为线段BE靠近点E的一个三等分点,点P在线段CD上移动.
矩形ABCD所在平面垂直于三角形ABE所在平面,AB=2AE=3,AD=2,∠ABE=30°,点F为线段BE靠近点E的一个三等分点,点P在线段CD上移动.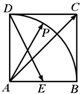 在正方形ABCD中,E为AB的中点,P为以A为圆心,AB为半径的圆弧上的任意一点,设向量$\overrightarrow{AC}=λ\overrightarrow{DE}+μ\overrightarrow{AP}$,当∠PAB=$\frac{π}{3}$时,λ+μ=2,当∠PAB∈[0,$\frac{π}{2}$]时,λ+μ的最小值为$\frac{1}{2}$.
在正方形ABCD中,E为AB的中点,P为以A为圆心,AB为半径的圆弧上的任意一点,设向量$\overrightarrow{AC}=λ\overrightarrow{DE}+μ\overrightarrow{AP}$,当∠PAB=$\frac{π}{3}$时,λ+μ=2,当∠PAB∈[0,$\frac{π}{2}$]时,λ+μ的最小值为$\frac{1}{2}$.