Question

9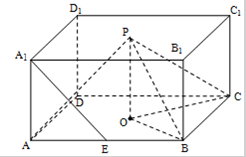．如图，P、O分别是正四棱柱ABCD-A₁B₁C₁D₁上、下底中心，E是AB的中点，AB=kAA₁=2$\sqrt{2}$．
（1）求证：A₁E∥平面PBC₁；
（2）当k=$\sqrt{2}$时，求点O到平面PBC的距离．

Answer 1

分析 （1）依题意，设此棱柱的高AA₁=2，则AB=2k，以O为原点建立空间直角坐标系，写出相关点的坐标和相关向量的坐标，取BC中点F，得$\overrightarrow{PF}$=$\overrightarrow{{A}_{1}E}$，利用线面平行的判定定理证明即可；
（2）利用等体积，即可求点O到平面PBC的距离．

解答 （1）证明：设此棱柱的高AA₁=2，则AB=2k，如图建立空间直角坐标系：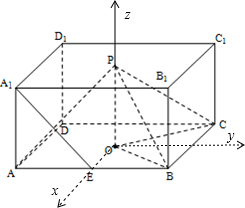
则P（0，0，2），O（0，0，0），B（k，k，0），C（-k，k，0），A₁（k，-k，2），A（k，-k，0），E（k，0，0）
取BC中点F（0，k，0）
则$\overrightarrow{PF}$=（0，k，-2），$\overrightarrow{{A}_{1}E}$=（0，k，-2），
∴$\overrightarrow{PF}$=$\overrightarrow{{A}_{1}E}$
∴A₁E∥PF，PF?面PBC，A₁E?面PBC
∴A₁E∥平面PBC；
（2）解：当k=$\sqrt{2}$时，AB=2$\sqrt{2}$，AA₁=2，
∴V_P-OBC=$\frac{1}{3}×\frac{1}{2}×2\sqrt{2}×\sqrt{2}×2$=$\frac{4}{3}$，
∵S_△PBC=$\frac{1}{2}×2\sqrt{2}×\sqrt{3}$=$\sqrt{6}$，
设点O到平面PBC的距离为h，则$\frac{1}{3}×\sqrt{6}h$=$\frac{4}{3}$，
∴h=$\frac{2\sqrt{6}}{3}$．

点评 本题综合考查了线面平行的判定定理，点O到平面PBC的距离，考查学生分析解决问题的能力，属于中档题．