题目内容
已知动点M的坐标满足方程13
=|12x+5y-12|,则动点M的轨迹是( )
| x2+y2 |
分析:把已知方程变形为
=
,此式满足抛物线的定义,从而可选出答案.
| x2+y2 |
| |12x+5y-12| |
| 13 |
解答:解:∵动点M的坐标满足方程13
=|12x+5y-12|,变形为
=
,
∴上式表示的是动点M(x,y)到定点(0,0)与定直线12x+5y-12=0的距离相等且定点不在定直线上,
根据抛物线的定义可知:动点的轨迹是以定点为焦点,定直线为准线的一条抛物线.
故选A.
| x2+y2 |
| x2+y2 |
| |12x+5y-12| |
| 13 |
∴上式表示的是动点M(x,y)到定点(0,0)与定直线12x+5y-12=0的距离相等且定点不在定直线上,
根据抛物线的定义可知:动点的轨迹是以定点为焦点,定直线为准线的一条抛物线.
故选A.
点评:理解抛物线的定义是解题的前提.其变形也很重要.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
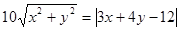 ,则动点M的轨迹方程是
,则动点M的轨迹方程是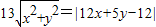 ,则动点M的轨迹是( )
,则动点M的轨迹是( )