题目内容
设函数f(x)=sin(ωx+φ)(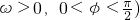 ,若将f(x)的图象沿x轴向右平移
,若将f(x)的图象沿x轴向右平移 个单位长度,得到的图象经过坐标原点;若将f(x)的图象上所有点的横坐标缩短到原来的
个单位长度,得到的图象经过坐标原点;若将f(x)的图象上所有点的横坐标缩短到原来的 倍(纵坐标不变),得到的图象关于直线
倍(纵坐标不变),得到的图象关于直线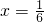 对称.则
对称.则
- A.
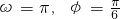
- B.
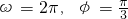
- C.
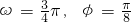
- D.
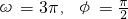
A
分析:依题意,f(x- )=sin[(ω(x-
)=sin[(ω(x- )+φ)],f(2x)=sin(2ωx+φ)的图象关于直线x=
)+φ)],f(2x)=sin(2ωx+φ)的图象关于直线x= 对称,由此二式可求得答案.
对称,由此二式可求得答案.
解答:∵f(x)=sin(ωx+φ)的图象沿x轴向右平移 个单位长度,得到的图象经过坐标原点,
个单位长度,得到的图象经过坐标原点,
即f(x- )=sin[(ω(x-
)=sin[(ω(x- )+φ)]的图象经过原点,
)+φ)]的图象经过原点,
∴sin(φ- ω)=0,
ω)=0,
∴φ- ω=kπ①;
ω=kπ①;
又f(2x)=sin(2ωx+φ)的图象关于直线x= 对称,
对称,
∴2ω× +φ=kπ+
+φ=kπ+ ,(k∈Z)②
,(k∈Z)②
不妨令①②中的k=0,得:ω=π,φ= ,符合ω>0,0<φ<
,符合ω>0,0<φ< .
.
故选A.
点评:本题考查函数y=Asin(ωx+φ)的图象变换,理解题意得到关于ω、φ的两个关系式是关键,也是难点,属于难题.
分析:依题意,f(x-
 )=sin[(ω(x-
)=sin[(ω(x- )+φ)],f(2x)=sin(2ωx+φ)的图象关于直线x=
)+φ)],f(2x)=sin(2ωx+φ)的图象关于直线x= 对称,由此二式可求得答案.
对称,由此二式可求得答案.解答:∵f(x)=sin(ωx+φ)的图象沿x轴向右平移
 个单位长度,得到的图象经过坐标原点,
个单位长度,得到的图象经过坐标原点,即f(x-
 )=sin[(ω(x-
)=sin[(ω(x- )+φ)]的图象经过原点,
)+φ)]的图象经过原点,∴sin(φ-
 ω)=0,
ω)=0,∴φ-
 ω=kπ①;
ω=kπ①;又f(2x)=sin(2ωx+φ)的图象关于直线x=
 对称,
对称,∴2ω×
 +φ=kπ+
+φ=kπ+ ,(k∈Z)②
,(k∈Z)②不妨令①②中的k=0,得:ω=π,φ=
 ,符合ω>0,0<φ<
,符合ω>0,0<φ< .
.故选A.
点评:本题考查函数y=Asin(ωx+φ)的图象变换,理解题意得到关于ω、φ的两个关系式是关键,也是难点,属于难题.

练习册系列答案
相关题目