Question

已知∠AOB=90°内有一动点P，PM⊥OA于M，PN⊥OB于N，且四边形PMON的面积等于4，今以O为原点，∠AOB的平分线Ox为极轴(如图)，求动点P的轨迹方程.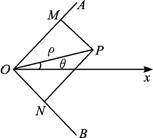

Answer 1

解析：设P点坐标为(ρ,θ)，

∴∠POM=45°-θ,∠NOP=45°+θ,

故四边形PMON的面积

S=OM·PM+ON·PN

=［cos(45°-θ)·sin(45°-θ)+cos(45°+θ)sin(45°+θ)］

=［sin (90°-2θ)+sin(90°+2θ)］=4.

∴ρ²·cos2θ=8为P点极坐标方程,

若化为直角坐标方程即x²-y²=8，是双曲线右支.