题目内容
已知∠AOB=90°,C为空间中一点,且∠AOC=∠BOC=60°,则直线OC与平面AOB所成角的正弦值为分析:由对称性点C在平面AOB内的射影D必在∠AOB的平分线上,作DE⊥OA于E,根据线面所成角的定义可知∠COD为直线OC与平面AOB所成角,在三角形COD中求解此角即可.
解答: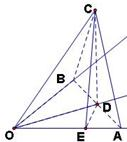 解:由对称性点C在平面AOB内的射影D必在∠AOB的平分线上
解:由对称性点C在平面AOB内的射影D必在∠AOB的平分线上
作DE⊥OA于E,连接CE则由三垂线定理CE⊥OE,
设DE=1?OE=1,OD=
,又∠COE=60°,CE⊥OE?OC=2,
所以CD=
=
,
因此直线OC与平面AOB所成角的正弦值sin∠COD=
.
 解:由对称性点C在平面AOB内的射影D必在∠AOB的平分线上
解:由对称性点C在平面AOB内的射影D必在∠AOB的平分线上作DE⊥OA于E,连接CE则由三垂线定理CE⊥OE,
设DE=1?OE=1,OD=
| 2 |
所以CD=
| OC2-OD2 |
| 2 |
因此直线OC与平面AOB所成角的正弦值sin∠COD=
| ||
| 2 |
点评:本题主要考查了直线与平面所成角,以及三垂线定理,考查空间想象能力、运算能力和推理论证能力,属于基础题.

练习册系列答案
相关题目