题目内容
若函数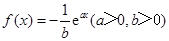 的图象在
的图象在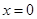 处的切线与圆
处的切线与圆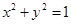 相切,则
相切,则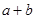 的最大值是( )
的最大值是( )
| A.4 | B. | C.2 | D. |
D
解析试题分析:函数 的导数为
的导数为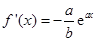 ,所以在
,所以在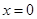 处的切线斜率为
处的切线斜率为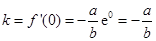 ,又
,又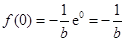 ,即切点为
,即切点为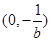 ,所以切线方程为
,所以切线方程为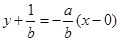 ,即
,即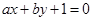 .圆心到直线
.圆心到直线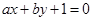 的距离
的距离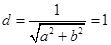 ,即
,即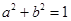 ,设
,设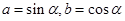 ,则
,则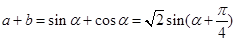 ,所以
,所以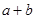 的最大值是
的最大值是 .
.
考点:1.导数的几何意义;2.直线与圆的关系;3.基本不等式求最值.

练习册系列答案
 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
若存在过点(1,0)的直线与曲线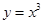 和
和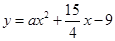 都相切,则
都相切,则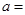 ( )
( )
A.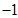 或 或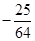 | B.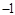 或 或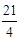 | C.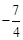 或 或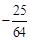 | D.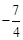 或 或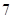 |
函数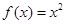 在点
在点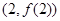 处的切线方程为( )
处的切线方程为( )
A.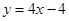 | B.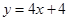 | C.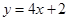 | D.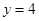 |
定义在 上的函数
上的函数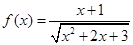 ,则
,则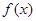 ( )
( )
| A.既有最大值也有最小值 | B.既没有最大值,也没有最小值 |
| C.有最大值,但没有最小值 | D.没有最大值,但有最小值 |
设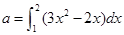 ,则二项式
,则二项式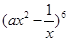 展开式中的第四项为( )
展开式中的第四项为( )
A.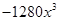 | B.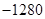 | C. | D.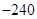 |
曲线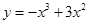
 在点(1,2)处的切线方程为( )
在点(1,2)处的切线方程为( )
| A.y=3x-1 | B.y=-3x+5 | C.y=3x+5 | D.y=2x |
设曲线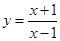 在点
在点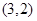 处的切线与直线
处的切线与直线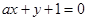 垂直,则
垂直,则 等于 ( )
等于 ( )
A.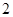 | B. | C. | D.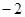 |
已知函数 在
在 上满足
上满足 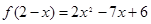 ,则曲线
,则曲线 在
在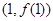 处的切线方程是( )
处的切线方程是( )
A.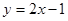 | B.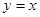 | C.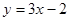 | D.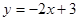 |
函数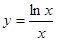 的最大值为( )
的最大值为( )
A.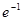 | B.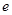 | C.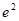 | D. |