题目内容
已知点![]() ,
,![]() ,动点
,动点![]() 的轨迹曲线
的轨迹曲线![]() 满足
满足![]() ,
,![]() ,过点
,过点![]() 的直线交曲线
的直线交曲线![]() 于
于![]() 、
、![]() 两点.
两点.
(1)求![]() 的值,并写出曲线
的值,并写出曲线![]() 的方程;
的方程;
(2)求△![]() 面积的最大值.
面积的最大值.
【命题意图】本小题考查椭圆的定义及标准方程,直线和椭圆的综合应用,考查学生的逻辑思维能力和运算求解能力.
【试题解析】解:(1)设![]() ,在△
,在△![]() 中,
中,![]() ,
,![]() ,根据余弦定理得
,根据余弦定理得![]() . (2分)
. (2分)
即![]() .
.
![]() .
.
而![]() ,所以
,所以![]() .
.
所以![]() . (4分)
. (4分)
又![]() ,
,
因此点![]() 的轨迹是以
的轨迹是以![]() 、
、![]() 为焦点的椭圆(点
为焦点的椭圆(点![]() 在
在![]() 轴上也符合题意),
轴上也符合题意),
![]() ,
,![]() .
.
所以曲线![]() 的方程为
的方程为![]() . (6分)
. (6分)
(2)设直线![]() 的方程为
的方程为![]() .
.
由 ,消去x并整理得
,消去x并整理得![]() . ①
. ①
显然方程①的![]() ,设
,设![]() ,
,![]() ,则
,则![]()
由韦达定理得![]() ,
,![]() . (9分)
. (9分)
所以![]() .
.
令![]() ,则
,则![]() ,
, .
.
由于函数![]() 在
在![]() 上是增函数.
上是增函数.
所以![]() ,当
,当![]() ,即
,即![]() 时取等号.
时取等号.
所以 ,即
,即![]() 的最大值为3.
的最大值为3.
所以△![]() 面积的最大值为3,此时直线
面积的最大值为3,此时直线![]() 的方程为
的方程为![]() . (12分)
. (12分)

练习册系列答案
相关题目
 是⊙
是⊙ :
: 上的任意一点,过
上的任意一点,过 垂直
垂直 轴于
轴于 ,动点
,动点 满足
满足 。
。 ,在动点
,在动点 、
、 ,使
,使 (O是坐标原点),若存在,求出直线
(O是坐标原点),若存在,求出直线 的方程,若不存在,请说明理由。
的方程,若不存在,请说明理由。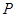 是⊙
是⊙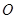 :
: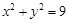 上的任意一点,过
上的任意一点,过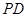 垂直
垂直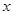 轴于
轴于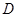 ,动点
,动点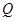 满足
满足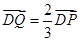 。
。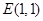 ,在动点
,在动点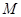 、
、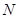 ,使
,使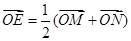 (O是坐标原点),若存在,求出直线
(O是坐标原点),若存在,求出直线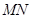 的方程,若不存在,请说明理由
的方程,若不存在,请说明理由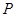 是⊙
是⊙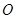 :
: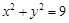 上的任意一点,过
上的任意一点,过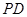 垂直
垂直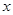 轴于
轴于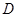 ,动点
,动点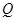 满足
满足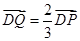 。
。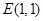 ,在动点
,在动点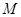 、
、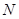 ,使
,使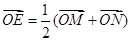 (O是坐标原点),若存在,求出直线
(O是坐标原点),若存在,求出直线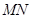 的方程,若不存在,请说明理由。
的方程,若不存在,请说明理由。