题目内容
20．某人从点A向东位移60m到达点B，又从点B向东偏北30°方向位移50m到达C点，又从点C向北偏东60°方向位移30m到达D点，选用适当的比例尺作图，求点D相对于点A的位置．分析 根据题意，画出图形，结合图形，利用三角形的正弦、余弦定理，求出AD的值以及点D在点A的方向是什么．
解答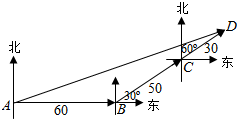 
解：根据题意，画出图形，如图所示；
则点B、C、D在同一直线上，且∠ABD=150°，
又AC=60，BD=50+30=80，
∴AD2=AB2+BD2-2AB•BDcos150°
=502+802-2×50×80×（-$\frac{\sqrt{3}}{2}$）
=8900+4000$\sqrt{3}$，
∴AD=$\sqrt{8900+4000\sqrt{3}}$=10$\sqrt{89+40\sqrt{3}}$≈125.8；
又$\frac{BD}{sin∠BAD}$=$\frac{AD}{sin∠ABD}$，
∴sin∠BAD=$\frac{80•sin150°}{125.8}$≈0.3180，
∴∠BAD≈18.4°，
∴点D在点A的东偏北18.4°，距离125.8m处的位置．
点评 本题考查了方向向量的应用问题，也考查了正弦、余弦定理的应用问题，是综合性题目．
练习册系列答案
相关题目
11．某高中学校共有学生2000名，各年级男、女人数如下表：
已知从全校学生中随机抽取1名，抽到高二年级女生的概率是0.19．
（1）求x的值；
（2）已知y≥245，z≥245，且在高三年级任意抽取一人，抽到男生的概率大于抽到女生的概率，试写出y、z所有取值．
| 高一年级 | 高二年级 | 高三年级 | |
| 女生 | 373 | X | Y |
| 男生 | 377 | 370 | z |
（1）求x的值；
（2）已知y≥245，z≥245，且在高三年级任意抽取一人，抽到男生的概率大于抽到女生的概率，试写出y、z所有取值．
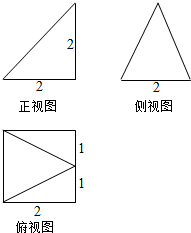如图是一个几何体的三视图，根据图中所给的数据，求这个几何体的表面积和体积．