题目内容
已知直线l: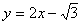 与椭圆C:
与椭圆C: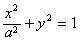 (a>1)交于P,Q两点。
(a>1)交于P,Q两点。
(1)设PQ中点M(x0,y0),求证: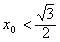 ;
;
(2)椭圆C的右顶点为A,且A在以PQ为直径的圆上,求△OPQ的面积(O为坐标原点)。
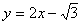 与椭圆C:
与椭圆C: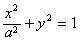 (a>1)交于P,Q两点。
(a>1)交于P,Q两点。(1)设PQ中点M(x0,y0),求证:
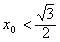 ;
;(2)椭圆C的右顶点为A,且A在以PQ为直径的圆上,求△OPQ的面积(O为坐标原点)。
解:(1)设直线l与椭圆C交于P(x1,y1),Q(x2,y2)
将 代入x2+a2y2-a2=0,
代入x2+a2y2-a2=0,
整理可得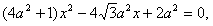
由韦达定理得
∵M(x0,y0)为PQ中点,
∴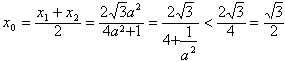
故 。
。
(2)依题意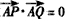
得(x1-a)(x2-a)+y1y2=0
又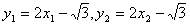
∴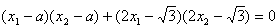
整理可得5x1·x2-(2 +a)(x1+x2)+a2+3=0, ②
+a)(x1+x2)+a2+3=0, ②
将①代入②得
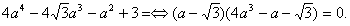
∵a>1,则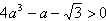
∴
故所求椭圆方程为
联立椭圆与直线方程得
∴
原点到直线的距离为
∴ 。
。
将
 代入x2+a2y2-a2=0,
代入x2+a2y2-a2=0,整理可得
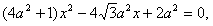
由韦达定理得

∵M(x0,y0)为PQ中点,
∴
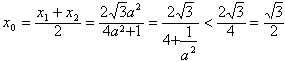
故
 。
。(2)依题意
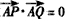
得(x1-a)(x2-a)+y1y2=0
又
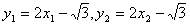
∴
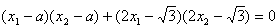
整理可得5x1·x2-(2
 +a)(x1+x2)+a2+3=0, ②
+a)(x1+x2)+a2+3=0, ② 将①代入②得

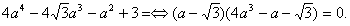
∵a>1,则
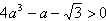
∴

故所求椭圆方程为

联立椭圆与直线方程得

∴

原点到直线的距离为

∴
 。
。
练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案
相关题目
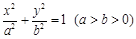 ,其离心率为
,其离心率为 ,经过椭圆焦点且垂直于长轴的弦长为3.
,经过椭圆焦点且垂直于长轴的弦长为3. 与椭圆C交于A、B两点,P为椭圆上的点,O为坐标原点,且满足
与椭圆C交于A、B两点,P为椭圆上的点,O为坐标原点,且满足 ,求
,求 的取值范围.
的取值范围.