题目内容
 (2012•丹东模拟)已知x=
(2012•丹东模拟)已知x=| π |
| 6 |
| 1 |
| 2 |
(Ⅰ)求a的值;
(Ⅱ)作出函数f(x)在x∈[0,π]上的图象简图(不要求书写作图过程).
分析:(Ⅰ)由题意可得f(0)=f(
),即
=
a•sin
+
cos
,由此求得a的值.
(Ⅱ)由a=
,可得f(x)=
•sin2x+
cos2x=2sin(2x+
),其图象如图所示.
| π |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2π |
| 3 |
| 1 |
| 2 |
| 2π |
| 3 |
(Ⅱ)由a=
| 3 |
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| π |
| 6 |
解答:解:(Ⅰ)∵x=
是函数f(x)=(asinx+cosx)cosx-
的图象的一条对称轴,且f(x)=
a•sin2x+
-
=
a•sin2x+
cos2x,
∴f(0)=f(
),即
=
a•sin
+
cos
,解得 a=
.
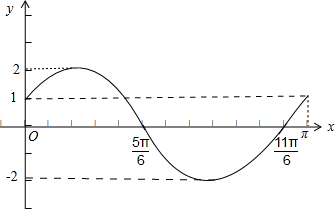
(Ⅱ)∵a=
,∴f(x)=
×
•sin2x+
cos2x=2sin(2x+
),其图象如图所示:
| π |
| 6 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1+cos2x |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴f(0)=f(
| π |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2π |
| 3 |
| 1 |
| 2 |
| 2π |
| 3 |
| 3 |
(Ⅱ)∵a=
| 3 |
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| π |
| 6 |

点评:本题主要考查三角函数的恒等变换及化简求值,函数的对称性的应用,用五点法作y=Asin(ωx+∅)的图象,属于中档题.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
 (2012•丹东模拟)如图,⊙O是△ABC的外接圆,D是弧AC的中点,BD交AC于E.
(2012•丹东模拟)如图,⊙O是△ABC的外接圆,D是弧AC的中点,BD交AC于E.