题目内容
20．已知等差数列{an}和{bn}的前n项和分别为An和Bn，若$\frac{{A}_{n}}{{B}_{n}}$=$\frac{3n-1}{2n+3}$，则$\frac{{a}_{13}}{{b}_{13}}$的值为$\frac{74}{53}$．分析 由等差数列的性质和求和公式可得$\frac{{a}_{13}}{{b}_{13}}$=$\frac{{A}_{25}}{{B}_{25}}$，代值计算可得．
解答 解：由等差数列的性质和求和公式可得：
$\frac{{a}_{13}}{{b}_{13}}$=$\frac{2{a}_{13}}{2{b}_{13}}$=$\frac{{a}_{1}+{a}_{25}}{{b}_{1}+{b}_{25}}$=$\frac{\frac{25（{a}_{1}+{a}_{25}）}{2}}{\frac{25（{b}_{1}+{b}_{25}）}{2}}$
=$\frac{{A}_{25}}{{B}_{25}}$=$\frac{3×25-1}{2×25+3}$=$\frac{74}{53}$
故答案为：$\frac{74}{53}$
点评 本题考查等差数列的求和公式和性质，属中档题．
练习册系列答案
全优点练单元计划系列答案
相关题目
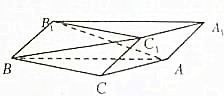如图，斜三棱柱ABC-A1B1C1的底面是直角三角形，∠ACB=90°，点B1在底面内的射影恰好是BC的中点，且BC=CA=2，
8．数列{an}满足lg2an=lg4${\;}^{\sqrt{{a}_{n-1}}}$+1，a1=1
（1）求{an}通项公式．
（2）求1+5+9+13+…+（8n-7）=（4n-3）（2n-1）．．
（1）求{an}通项公式．
（2）求1+5+9+13+…+（8n-7）=（4n-3）（2n-1）．．