题目内容
当实数t取什么值时,复数z=
+
i的幅角主值θ适合0≤θ≤
?
| |cost| |
| |sint| |
| π |
| 4 |
因为复数z=
+
i的实部与虚部都是非负数,
所以z的幅角主值θ一定适合0≤θ≤
从而0≤θ≤
?0≤tgθ≤1.
显然r=|z|≠0因为tgθ=
=
,所以0≤tgθ≤1?0≤|tgθ|≤1?-1≤tgt≤1.
由于
y=tgt在-
<t<
内是增函数,并且它的周期是π,
因此-1≤tgt≤1的解是kπ-
≤t≤kπ+
(k为任意整数).
这就是所求的实数t的取值范围
| |cost| |
| |sint| |
所以z的幅角主值θ一定适合0≤θ≤
| π |
| 2 |
从而0≤θ≤
| π |
| 4 |
显然r=|z|≠0因为tgθ=
| ||
|
| |tgt| |
由于
y=tgt在-
| π |
| 2 |
| π |
| 2 |
因此-1≤tgt≤1的解是kπ-
| π |
| 4 |
| π |
| 4 |
这就是所求的实数t的取值范围

练习册系列答案
相关题目
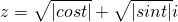 的幅角主值θ适合
的幅角主值θ适合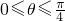 ?
?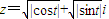 的幅角主值θ适合
的幅角主值θ适合 ?
?