题目内容
(2006•安徽)设常数a>0,(ax2+
)4展开式中x3的系数为
,则
(a+a2+…+an)=
| 1 | ||
|
| 3 |
| 2 |
| lim |
| n→∞ |
1
1
.分析:先利用展开式中x3的系数为
,求出a的值,再利用无穷等比数列和的极限公式求解.
| 3 |
| 2 |
解答:解:由题意,展开式的通项为Tr+1=
×a4-r×x8-
r
令8-
r=3,则r=2
∵(ax2+
)4展开式中x3的系数为
,
∴6a2=
∵a>0,
∴a=
∴
(a+a2+…+an)=
=1
故答案为:1.
| C | r 4 |
| 5 |
| 2 |
令8-
| 5 |
| 2 |
∵(ax2+
| 1 | ||
|
| 3 |
| 2 |
∴6a2=
| 3 |
| 2 |
∵a>0,
∴a=
| 1 |
| 2 |
∴
| lim |
| n→∞ |
| ||
1-
|
故答案为:1.
点评:本题以二项式为载体,考查数列的极限,关键是利用展开式中x3的系数为
,求出a的值,从而求极限.
| 3 |
| 2 |

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
(2006
安徽,4)设a、b R,已知命题p∶a=b;命题
R,已知命题p∶a=b;命题 ,则p是q成立的
,则p是q成立的
[
]|
A .必要不充分条件 |
B .充分不必要条件 |
|
C .充分必要条件 |
D .既不充分也不必要条件 |
 的前n项和为
的前n项和为 ,已知
,已知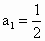 ,
, ,n=1,2,….
,n=1,2,….
 的递推关系式(n≥2),并求
的递推关系式(n≥2),并求 ,
, ,求数列
,求数列 的前n项和
的前n项和 .
. 在R上有定义,对任何实数
在R上有定义,对任何实数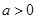 和任何实数
和任何实数 ,都有
,都有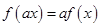
 ;
; 其中
其中 和
和 均为常数;
均为常数; 时,设
时,设 ,讨论
,讨论 在
在 内的单调性并求极值.
内的单调性并求极值.