题目内容
已知tanθ＞1，且sinθ+cosθ＜0，则cosθ的取值范围是
- A.
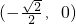
- B.
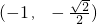
- C.
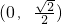
- D.
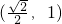
A
分析：先由已知中tanθ＞1，sinθ+cosθ＜0判断角所在的象限，从而判断再由sinθ和cosθ符号及大小关系．进而可得到答案．
解答：∵tanθ＞1，
∴θ的终边在第一或第三象限，
又sinθ+cosθ＜0，
∴θ的终边在第三象限，
则2kπ+
＜x＜2kπ+
，k∈Z
∴-
＜cosθ＜0，
故选 A．
点评：本题考查三角函数在各个象限中的符号及大小关系，及三角函数值的符号，其中根据已知条件判断出θ角的范围是解答本题的关键．
分析：先由已知中tanθ＞1，sinθ+cosθ＜0判断角所在的象限，从而判断再由sinθ和cosθ符号及大小关系．进而可得到答案．
解答：∵tanθ＞1，
∴θ的终边在第一或第三象限，
又sinθ+cosθ＜0，
∴θ的终边在第三象限，
则2kπ+
＜x＜2kπ+，k∈Z∴-
＜cosθ＜0，故选 A．
点评：本题考查三角函数在各个象限中的符号及大小关系，及三角函数值的符号，其中根据已知条件判断出θ角的范围是解答本题的关键．
练习册系列答案
浙江名校名师金卷系列答案
全优冲刺100分系列答案
相关题目
已知tanθ＞1，且sinθ+cosθ＜0，则cosθ的取值范围是（ ）
A、(-
| ||||
B、(-1， -
| ||||
C、(0，
| ||||
D、(
|
＋cos
，0)
)
)
，1)