题目内容
设P是椭圆
上的一点，F1，F2是椭圆的两个焦点，则|PF1||PF2|的最大值为________；最小值为________．
4 1
分析：|PF1|•|PF2|=（a-ex）（a+ex）=a2-e2x2，根据二次函数，由此可求出|PF1|•|PF2|的最大值和最小值．
解答：由焦半径公式|PF1|=a-ex，|PF2|=a+ex
|PF1|•|PF2|=（a-ex）（a+ex）=a2-e2x2=-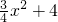
∵x∈[-2，2]
∴当x=0时，|PF1|•|PF2|的最大值是4
当x=2或-2时，|PF1|•|PF2|的最小值是1
答案：4，1．
点评：本题考查了椭圆的性质，正确解题的关键是列出|PF1|•|PF2|的代数式，本题中运用二次函数的求最值．
分析：|PF1|•|PF2|=（a-ex）（a+ex）=a2-e2x2，根据二次函数，由此可求出|PF1|•|PF2|的最大值和最小值．
解答：由焦半径公式|PF1|=a-ex，|PF2|=a+ex
|PF1|•|PF2|=（a-ex）（a+ex）=a2-e2x2=-
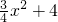
∵x∈[-2，2]
∴当x=0时，|PF1|•|PF2|的最大值是4
当x=2或-2时，|PF1|•|PF2|的最小值是1
答案：4，1．
点评：本题考查了椭圆的性质，正确解题的关键是列出|PF1|•|PF2|的代数式，本题中运用二次函数的求最值．
练习册系列答案
名校课堂系列答案
相关题目
上的一点，F是椭圆的左焦点，且
，
，则点P到该椭圆左准线的距离为 （ ） 
B．3
上的一点，F1、F2是焦点，若∠F1PF2=60°，则△PF1F2的面积为________．
上的一点，F1、F2是焦点，若∠F1PF2=30°，则△PF1F2的面积为（ ）
上的一点，F1，F2是椭圆的两个焦点，则|PF1||PF2|的最大值为 ；最小值为 ．