题目内容
设P是椭圆 上的一点,F1、F2是焦点,若∠F1PF2=60°,则△PF1F2的面积为________.
上的一点,F1、F2是焦点,若∠F1PF2=60°,则△PF1F2的面积为________.
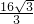
分析:根据椭圆的定义,得PF1+PF2=2a=10…①,再在△F1PF2中用余弦定理,得PF12+PF22-PF1•PF2=36…②.由①②联解,得PF1•PF2=
 ,最后用根据正弦定理关于面积的公式,可得△PF1F2的面积.
,最后用根据正弦定理关于面积的公式,可得△PF1F2的面积.解答:∵椭圆方程是
 ,
,∴a2=25,b2=16.可得a=5,c2=25-16=9,即c=3.
∵P是椭圆
 上的一点,F1、F2是焦点,
上的一点,F1、F2是焦点,∴根据椭圆的定义,得PF1+PF2=2a=10…①
又∵△F1PF2中,∠F1PF2=60°且F1F2=2c=6
∴根据余弦定理,得F1F22=PF12+PF22-2PF1•PF2cos60°=36
即PF12+PF22-PF1•PF2=36…②
∴①②联解,得PF1•PF2=

根据正弦定理,得△PF1F2的面积为:S=
 PF1•PF2sin60°=
PF1•PF2sin60°=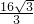
故答案为:
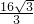
点评:本题给出椭圆上一点对两个焦点的张角为60度,求椭圆两焦点与该点构成三角形的面积,着重考查了椭圆的简单性质和正、余弦定理等知识点,属于中档题.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目

 上的一点,F1,F2是椭圆的两个焦点,则|PF1||PF2|的最大值为________;最小值为________.
上的一点,F1,F2是椭圆的两个焦点,则|PF1||PF2|的最大值为________;最小值为________. 上的一点,F1、F2是焦点,若∠F1PF2=30°,则△PF1F2的面积为( )
上的一点,F1、F2是焦点,若∠F1PF2=30°,则△PF1F2的面积为( )


 上的一点,F1,F2是椭圆的两个焦点,则|PF1||PF2|的最大值为 ;最小值为 .
上的一点,F1,F2是椭圆的两个焦点,则|PF1||PF2|的最大值为 ;最小值为 .