题目内容
(本题满分16分)数列 的前
的前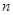 项和记为
项和记为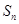 ,且满足
,且满足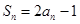 .
.
(1)求数列 的通项公式;
的通项公式;
(2)求和 ;
;
(3)设有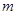 项的数列
项的数列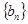 是连续的正整数数列,并且满足:
是连续的正整数数列,并且满足: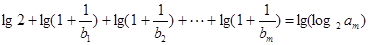 .
.
问数列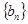 最多有几项?并求这些项的和.
最多有几项?并求这些项的和.
(1) (2)
(2) (3)数列
(3)数列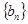 最多有9项,和为63.
最多有9项,和为63.
解析试题分析:(1)由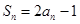 得
得 ,
,
相减得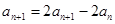 ,即
,即 .
.
又 ,得
,得 ,
,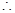 数列
数列 是以1为首项2为公比的等比数列,
是以1为首项2为公比的等比数列,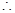
 . ……5分
. ……5分
(2)由(1)知 .
.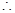



 . ……10分
. ……10分
(3)由已知得 .
.
又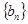 是连续的正整数数列,
是连续的正整数数列,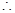
 .
.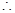 上式化为
上式化为 . ……12分
. ……12分
又 ,消
,消 得
得 .
. ,由于
,由于 ,
,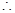
 ,
,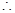
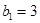 时,
时,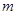 的最大值为9.
的最大值为9.
此时数列的所有项的和为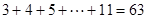 . ……16分
. ……16分
考点:本小题主要考查由数列的递推公式求数列的通项公式,以及公式法、分组法等求数列的前n项的和,考查学生转化问题的能力和运算求解能力.
点评:由数列的递推公式求数列的通项公式有累加、累乘和构造新数列法,求数列的前n项和有公式法、分组法、错位相减法和裂项相消法等.

练习册系列答案
 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
 的前
的前 项和为
项和为 ,
, ,
,
 ,等差数列
,等差数列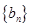 满足
满足 .
. ,求证
,求证 .
. 的前
的前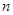 项和为
项和为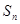 ,对一切正整数
,对一切正整数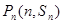 都在函数
都在函数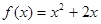 的图像上.
的图像上. 的通项公式;
的通项公式; ,求数列
,求数列 的通项公式.
的通项公式. 满足
满足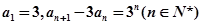 ,数列
,数列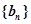 满足
满足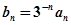 .
.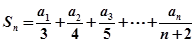 ,求满足不等式
,求满足不等式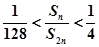 的所有正整数
的所有正整数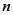 的值.
的值. 的前
的前 项和为
项和为 .已知
.已知 ,
,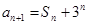 ,
, .
. ,求数列
,求数列 的通项公式;
的通项公式; ,
, ,求
,求 的取值范围.
的取值范围.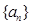 的前
的前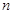 项和为
项和为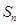 ,公差d
,公差d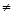 0,
0,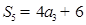 ,且
,且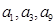 成等比数列.
成等比数列.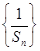 的前
的前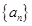 前
前 项和为
项和为 ,
,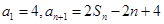 .
. 为等比数列;
为等比数列;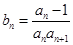 ,数列
,数列 前
前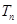 ,求证:
,求证: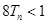 .
.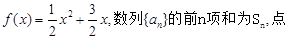
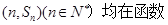
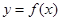
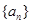 的通项公式
的通项公式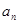 ;
; 求数列
求数列
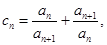 证明:
证明: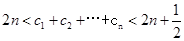 。
。 中,
中,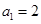 ,
,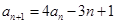 ,
,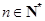 .
.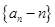 是等比数列;
是等比数列;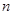 项和
项和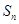 ;
;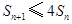 ,对任意
,对任意