题目内容
已知不等式ax2+x+c>0的解集为{x|1<x<3}.
(Ⅰ)求a,c的值;
(Ⅱ)若“ax2+2x+4c>0”是“x+m>0”的充分不必要条件,求实数m的取值范围.
(Ⅰ)求a,c的值;
(Ⅱ)若“ax2+2x+4c>0”是“x+m>0”的充分不必要条件,求实数m的取值范围.
(Ⅰ)依题意得,1、3是方程ax2+x+c=0的两根,且a<0,----------------------(1分)
所以,
---------------------------------------------------------(4分)
解得,
;---------------------------------------------------------(6分)
(Ⅱ)由(Ⅰ)得a=-
,c=-
,所以,ax2+2x+4c>0即为-
x2+2x-3>0,
解得,2<x<6,又x+m>0解得x>-m,-------------------------------------(8分)
∵“ax2+2x+4c>0”是“x+m>0”的充分不必要条件,
∴{x|2<x<6}?}x|x>-m},-----------------------------------(10分)
∴-m≤2,即m≥-2,
∴m的取值范围是[-2,+∞).------------------------(12分)
所以,
|
解得,
|
(Ⅱ)由(Ⅰ)得a=-
| 1 |
| 4 |
| 3 |
| 4 |
| 1 |
| 4 |
解得,2<x<6,又x+m>0解得x>-m,-------------------------------------(8分)
∵“ax2+2x+4c>0”是“x+m>0”的充分不必要条件,
∴{x|2<x<6}?}x|x>-m},-----------------------------------(10分)
∴-m≤2,即m≥-2,
∴m的取值范围是[-2,+∞).------------------------(12分)

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
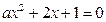 至少有一个负实根,
至少有一个负实根,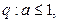 则q是p的( )
则q是p的( )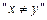 是
是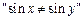 的( )
的( )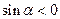 ,则“
,则“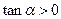 ”是“
”是“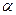 为第三象限角”的
为第三象限角”的