Question

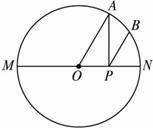
如图2-5-10，∠BAC的平分线与边BC和外接圆分别相交于D和E，延长AC交过D、E、C三点的圆于点F.

（1）求证：EF²=ED·EA；

（2）若AE=6，EF=3，求AF·AC的值.

图2-5-10

Answer 1

思路分析：（1）要证EF²=ED·EA，只需证△AEF∽△FED.（2）由于AC·AF=AD·AE，而由（1）可求得DE，因而AD可以求出来，从而计算出AD·AE，即为AC·AF的值.

（1）证明：连结CE、DF.

∵∠1=∠2，∠3=∠4，∠1=∠3，∴∠2=∠4.

∵∠AEF=∠FED，∴△AEF∽△FED.

∴.∴EF²=ED·EA.

（2）解：由（1）知EF²=AE·ED.

∵EF=3,AE=6,∴ED=.∴AD=.

∴AC·AF=AD·AE=6×=27.

    方法归纳 当题目中涉及两个圆时，我们常常作两圆的公共弦EC，以此来沟通两个圆的联系，这也是解决此类问题的关键.