题目内容
设Sn和Tn分别为两个等差数列{an}和{bn}的前n项和，若对任意n∈N，都有
=
，则数列{an}的第11项与数列{bn}的第11项的比是（ ）
| Sn |
| Tn |
| 7n+1 |
| 4n+27 |
| A、4：3 | B、3：2 |
| C、7：4 | D、78：71 |
分析：根据等差数列的前n项和的公式分别表示出S21和T21，然后根据等差数列的性质am+an=2a
，得到S21和T21的比等于数列{an}的第11项与数列{bn}的第11项的比，所以把n=21代入
=
中，求出的比值即为所求的比值．
| m+n |
| 2 |
| Sn |
| Tn |
| 7n+1 |
| 4n+27 |
解答：解：因为S21=
=21a11；同理Tn=
=21b11，
而
=
=
=
=
．
故选A
| 21(a1+a21) |
| 2 |
| 21(b1+b21) |
| 2 |
而
| S21 |
| T21 |
| 21a11 |
| 21b11 |
| a11 |
| b11 |
| 7×21+1 |
| 4×21+27 |
| 4 |
| 3 |
故选A
点评：此题考查学生掌握等差数列的前n项和的公式，灵活运用等差数列的性质化简求值，是一道高考常考的题型．
练习册系列答案
相关题目
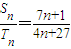，则第一个数列的第11项与第二个数列的第11项的比是 ．（说明：
．）
=
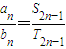，则数列{an}的第11项与数列{bn}的第11项的比是（ ）