题目内容
已知圆的方程x2+y2=25,点A为该圆上的动点,AB与x轴垂直,B为垂足,点P分![]() 的比λ=
的比λ=![]() .
.
⑴试求点P的轨迹E的方程; w.w.w⑵写出轨迹E的焦点坐标和准线方程.
解析:⑴设P(x,y)为所求轨迹上的任意一点,A(x1,y1),
则B点坐标为(x,0)………………………………………2分
由定比分点公式得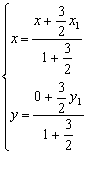
解得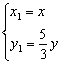 ,①………………………………6分
,①………………………………6分
∵点A在圆上,∴x12+y12=25 则![]() ,
,
即![]() (y≠0)…………………8分
(y≠0)…………………8分
⑵ 由⑴所求的方程![]() ,
,
可知轨迹E为以(4,0),(-4,0)为焦点,10为长轴的椭圆。
所以,焦点坐标为(4,0),(-4,0),准线方程为![]() ………………12分
………………12分

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
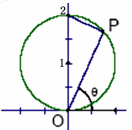
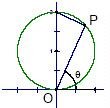 已知圆的方程x2+(y-1)2=1,P为圆上任意一点(不包括原点).直线OP的倾斜角为θ弧度,|OP|=d,则d=f(θ)的图象大致为
已知圆的方程x2+(y-1)2=1,P为圆上任意一点(不包括原点).直线OP的倾斜角为θ弧度,|OP|=d,则d=f(θ)的图象大致为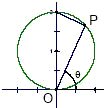 已知圆的方程x2+(y-1)2=1,P为圆上任意一点(不包括原点).直线OP的倾斜角为θ弧度,|OP|=d,则d=f(θ)的图象大致为________
已知圆的方程x2+(y-1)2=1,P为圆上任意一点(不包括原点).直线OP的倾斜角为θ弧度,|OP|=d,则d=f(θ)的图象大致为________