题目内容
烟囱向其周围地区散落烟尘而造成环境污染.已知A、B两座烟囱相距3km,其中A烟囱喷出的烟尘量是B烟囱的8倍,经环境检测表明:落在地面某处的烟尘浓度与该处到烟囱距离的平方成反比,而与烟囱喷出的烟尘量成正比.(比例系数为k).若C是连接两烟囱的线段AB上的点(不包括端点),设AC=xkm,C点的烟尘浓度记为y.(Ⅰ)写出y关于x的函数表达式;
(Ⅱ)是否存在这样的点C,使该点的烟尘浓度最低?若存在,求出AC的距离;若不存在,说明理由.
【答案】分析:(1)设B处烟尘量为1,则A处烟尘量为8,根据烟尘浓度与到烟囱距离的关系可求得A、B在C处的烟尘浓度,然后两者相加可得y关于x的函数.
(2)对(1)中函数进行求导,然后令导函数等于0求x的值,然后判断原函数的单调性进而可求得最小值.
解答:解:(1)设B处烟尘量为1,则A处烟尘量为8,
∴A在C处的烟尘浓度为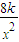
B在C处的烟尘浓度为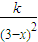 .其中0<x<3.
.其中0<x<3.
从而处总的烟尘浓度为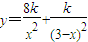 .(0<x<3);
.(0<x<3);
(2)由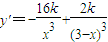 =
=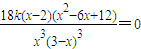 ,
,
解得x=2.
故当0<x<2时,y′<0,原函数单调递减.当2<x<3时y′>0,原函数单调递增.
∴x=2时,y取得极小值,且是最小值.
答:在连接西烟囱的线段AB上,距烟囱A处2km处的烟尘浓度最低.
点评:本题主要考查根据导数求函数的最值的问题.属基础题.
(2)对(1)中函数进行求导,然后令导函数等于0求x的值,然后判断原函数的单调性进而可求得最小值.
解答:解:(1)设B处烟尘量为1,则A处烟尘量为8,
∴A在C处的烟尘浓度为
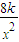
B在C处的烟尘浓度为
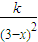 .其中0<x<3.
.其中0<x<3.从而处总的烟尘浓度为
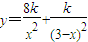 .(0<x<3);
.(0<x<3);(2)由
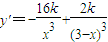 =
=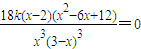 ,
,解得x=2.
故当0<x<2时,y′<0,原函数单调递减.当2<x<3时y′>0,原函数单调递增.
∴x=2时,y取得极小值,且是最小值.
答:在连接西烟囱的线段AB上,距烟囱A处2km处的烟尘浓度最低.
点评:本题主要考查根据导数求函数的最值的问题.属基础题.

练习册系列答案
 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
 (2007•湛江二模)烟囱向其周围地区散落烟尘造成环境污染.已知A、B两座烟囱相距20km,其中B烟囱喷出的烟尘量是A烟囱的8倍,经环境检测表明:落在地面某处的烟尘浓度与该处到烟囱距离的平方成反比,而与烟囱喷出的烟尘量成正比.(比例系数为k).若C是AB连线上的点,设AC=x km,C点的烟尘浓度记为y.
(2007•湛江二模)烟囱向其周围地区散落烟尘造成环境污染.已知A、B两座烟囱相距20km,其中B烟囱喷出的烟尘量是A烟囱的8倍,经环境检测表明:落在地面某处的烟尘浓度与该处到烟囱距离的平方成反比,而与烟囱喷出的烟尘量成正比.(比例系数为k).若C是AB连线上的点,设AC=x km,C点的烟尘浓度记为y.
