题目内容

过点A（-2，0）的直线交圆x2+y2=1交于P、Q两点，则
AP
•
AQ
的值为
3
3
．
分析：由题意可设直线PQ的方程为y=k（x+2），联立直线与圆的方程，设P（x1，y1），Q（x2，y2），根据方程的根与系数关系可求x1+x2，x1x2，进而可求y1y2=k2（x1+2）（x2+2），代入
AP
•
AQ
=（x1+2，y1）•（x2+2，y2）=x1x2+2（x1+x2）+y1y2+4即可求解
解答：解：由题意可设直线PQ的方程为y=k（x+2）
联立
y=k(x+2)
x2+y2=1
可得（1+k2）x2+4k2x+4k2-1=0
设P（x1，y1），Q（x2，y2），则x1+x2=
-4k2
1+k2
，x1x2=
4k2-1
1+k2

∴y1y2=k2（x1+2）（x2+2）=k2[x1x2+2（x1+x2）+4]
则
AP
•
AQ
=（x1+2，y1）•（x2+2，y2）
=x1x2+2（x1+x2）+y1y2+4
=（1+k2）x1x2+2(1+k2)(x1+x2)+4(1+k2)
=(1+k2)•
4k2-1
1+k2
+2(1+k2)•
-4k2
1+k2
+4+4k2
=4k2-1-8k2+4+4k2=3
故答案为：3
点评：本题主要考查了直线与圆的相交关系的应用，其中方程的根与系数关系的应用是求解问题的关键
练习册系列答案
相关题目
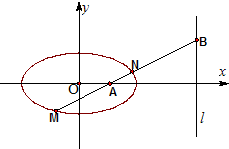精英家教网设椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）过点P(3，
3
4
7
)，且离心率e=
7
4
．
（Ⅰ）求椭圆C的方程；
（Ⅱ）过点A（2，0）的动直线AB交椭圆于点M、N，（其中点N位于点A、B之间），且交直线l：x=8于点B（如图）．证明：|
MA
|•|
NB
|=|
AN
|•|
MB
|．
已知两圆C1：x2+y2-2y=0，C2：x2+（y+1）2=4的圆心分别为C1，C2，P为一个动点，且直线PC1，PC2的斜率之积为-
12

（1）求动点P的轨迹M的方程；
（2）是否存在过点A（2，0）的直线l与轨迹M交于不同的两点C、D，使得|C1C|=|C1D|？若存在，求直线l的方程；若不存在，请说明理由．
如图，已知椭圆C：
x2
a2
+
y2
b2
=1(a＞b＞0)的焦点为F1（1，0）、F2（-1，0），离心率为
2
2
，过点A（2，0）的直线l交椭圆C于M、N两点．
（1）求椭圆C的方程；
（2）①求直线l的斜率k的取值范围；
②在直线l的斜率k不断变化过程中，探究∠MF1A和∠NF1F2是否总相等？若相等，请给出证明，若不相等，说明理由．
（2010•龙岩二模）过椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的一个焦点F且垂直于x轴的直线交椭圆于点(-1，
2
2
)．
（Ⅰ）求椭圆C的方程；
（Ⅱ）是否存在过点A（-2，0）的直线l与椭圆C交于两点M、N，使得|FP|=
1
2
|MN|（其中P为弦MN的中点）？若存在，求出直线l的方程；若不存在，请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网