题目内容

已知直线l为抛物线y2=2px（p＞0）的准线，F为其焦点，直线AB经过F且与抛物线交于A，B两点．过点A，B做直线l的垂线，垂足分别为C，D，线段CD的中点为M，O为坐标原点，则下列命题中错误的是（　　）
A、
CF
?
DF
=0
B、
MF
?
AB
=0
C、存在实数λ使得
OA
=λ
OD
D、三角形AMB为等腰三角形
分析：A、由于A，B在抛物线上，根据抛物线的定义可知CF=AF，DF=BF，从而由相等的角，由此可判断CF⊥DF；
B、取AB⊥x轴，则四边形ABDC为矩形，则可得结论；
C、取AB⊥x轴，则四边形ABDC为矩形，则可得结论；
D、取AB与x轴不垂直，则四边形ABDC为梯形，则可得结论．
解答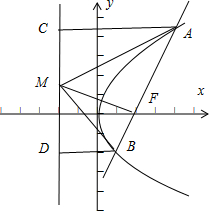：精英家教网解：A、由于A，B在抛物线上，根据抛物线的定义可知
抛物线上的点到焦点的距离等于其到准线的距离，即CA=AF，DB=BF，
因为C、D分别为A、B在l上的射影，所以CF⊥DF，故A正确；
B、取AB⊥x轴，则四边形ABDC为矩形，
则MF在X轴上，故MF⊥AB，故B正确；
C、取AB⊥x轴，则四边形ABDC为矩形，
则可知AD与CB交于原点，故AD过原点，则C正确；
D、如图知，若AB与x轴不垂直，则四边形ABDC为梯形，即得AC≠BD，
又由CM=MD，∠ACM=∠BDM，则AM≠BM，则D错误．
故答案为D．
点评：本题以抛物线为载体，考查抛物线的性质，解题的关键是合理运用抛物线的定义．
练习册系列答案
相关题目
精英家教网如图，已知直线l与抛物线y=
1
4
x2相切于点P（2，1），且与x轴交于点A，O为坐标原点，定点B的坐标为（2，0）．
（1）若动点M满足
AB
•
BM
+
2
|
AM
|=0，求动点M的轨迹C的方程；
（2）若过点B的直线l'（斜率不等于零）与（1）中的轨迹C交于不同
的两点E、F（E在B、F之间），且
BE
=λ
BF
，试求λ的取值范围．
给出下列命题：
①已知椭圆
x2
16
+
y2
8
=1的两个焦点为F1，F2，则这个椭圆上存在六个不同的点M，使得△F1MF2为直角三角形；
②已知直线l过抛物线y=2x2的焦点，且与这条抛物线交于A，B两点，则|AB|的最小值为2；
③若过双曲线C：
x2
a2
-
y2
b2
=1(a＞0，b＞0)的一个焦点作它的一条渐近线的垂线，垂足为M，O为坐标原点，则|OM|=a；
④已知⊙C1：x2+y2+2x=0，⊙C2：x2+y2+2y-1=0，则这两个圆恰有2条公切线．
其中正确命题的序号是
 
．（把你认为正确命题的序号都填上）
给出下列命题：
①已知椭圆
x2
16
+
y2
8
=1两焦点F1，F2，则椭圆上存在六个不同点M，使得△F1MF2为直角三角形；
②已知直线l过抛物线y=2x2的焦点，且与这条抛物线交于A，B两点，则|AB|的最小值为2；
③若过双曲线C：
x2
a2
-
y2
b2
=1（a＞0，b＞0）的一个焦点作它的一条渐近线的垂线，垂足为M，O为坐标原点，则|OM|=a；
④根据气象记录，知道荆门和襄阳两地一年中雨天所占的概率分别为20%和18%，两地同时下雨的概率为12%，则荆门为雨天时，襄阳也为雨天的概率是60%．
其中正确命题的序号是（　　）
给出下列命题：
①已知椭圆
x2
16
+
y2
8
=1的两个焦点为F1，F2，则这个椭圆上存在六个不同的点M，使得△F1MF2为直角三角形；
②已知直线l过抛物线y=2x2的焦点，且与这条抛物线交于A，B两点，则|AB|的最小值为2；
③若过双曲线C：
x2
a2
-
y2
b2
=1(a＞0，b＞0)的一个焦点作它的一条渐近线的垂线，垂足为M，O为坐标原点，则|OM|=a；
④已知⊙C1：x2+y2+2x=0，⊙C2：x2+y2+2y-1=0，则这两个圆恰有2条公切线．
其中正确命题的序号是______．（把你认为正确命题的序号都填上）
给出下列命题：
①已知椭圆的两个焦点为F1，F2，则这个椭圆上存在六个不同的点M，使得△F1MF2为直角三角形；
②已知直线l过抛物线y=2x2的焦点，且与这条抛物线交于A，B两点，则|AB|的最小值为2；
③若过双曲线C：的一个焦点作它的一条渐近线的垂线，垂足为M，O为坐标原点，则|OM|=a；
④已知⊙C1：x2+y2+2x=0，⊙C2：x2+y2+2y-1=0，则这两个圆恰有2条公切线．
其中正确命题的序号是    ．（把你认为正确命题的序号都填上）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网