题目内容
双曲线x2-y2=1左支上一点（a，b）到其渐近线y=x的距离是
，则a+b的值为 ．
【答案】分析：P（a，b）点在双曲线上，则有a2-b2=1，即（a+b）（a-b）=1．根据点到直线的距离公式能够求出a-b的值，上此能够得到a+b的值．
解答：解：P（a，b）点在双曲线上，则有a2-b2=1，即（a+b）（a-b）=1．
d=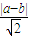
=
，
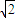∴|a-b|=2．
又P点在右支上，则有a＜b，
∴a-b=-2．
∴|a+b|×（-2）=1，a+b=-
，
故答案为：-
．
点评：本题考查双曲线的性质和点到直线的距离，解题时要注意公式的灵活运用．
解答：解：P（a，b）点在双曲线上，则有a2-b2=1，即（a+b）（a-b）=1．
d=
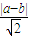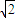=，∴|a-b|=2．
又P点在右支上，则有a＜b，
∴a-b=-2．
∴|a+b|×（-2）=1，a+b=-
，故答案为：-
．点评：本题考查双曲线的性质和点到直线的距离，解题时要注意公式的灵活运用．
练习册系列答案
小学学习好帮手系列答案
小学同步三练核心密卷系列答案
相关题目
若椭圆
+
=1过抛物线y2=8x的焦点，且与双曲线x2-y2=1有相同的焦点，则该椭圆的方程为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、x2+
|