题目内容
已知函数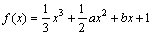
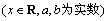 有极值,且在
有极值,且在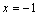 处的切线与直线
处的切线与直线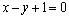 平行.
平行.
(1)求实数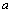 的取值范围.
的取值范围.
(2)是否存在实数a,使得
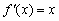 的两个根
的两个根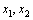 满足
满足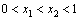 ,若存在,求实数a的取值范围;若不存在,请说明理由.
,若存在,求实数a的取值范围;若不存在,请说明理由.
【答案】
解:(1)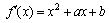 (1分)
(1分)
因为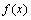 有极值,
有极值,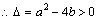 (*) (2分)
(*) (2分)
又在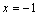 处的切线与直线
处的切线与直线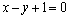 平行,
平行,
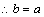 代入(*)式得,
代入(*)式得,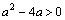 ,
,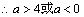 (6分)
(6分)
(2)假若存在实数a,使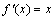 的两个根x1、x2满足
的两个根x1、x2满足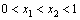 ,
,
即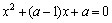 的两个根x1、x2满足0<x1<x2<1,
的两个根x1、x2满足0<x1<x2<1,
令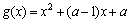 ,则有:
,则有: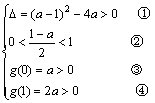 解之得
解之得
∴存在实数a,且 使是
使是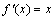 的两个根满足
的两个根满足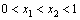 .
.

练习册系列答案
相关题目
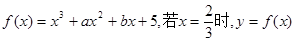 有极值,且曲线
有极值,且曲线 处的切线斜率为3.
处的切线斜率为3.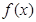 的解析式;
的解析式;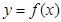 在
在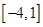 上的最大值和最小值.
上的最大值和最小值.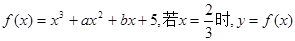 有极值,且曲线
有极值,且曲线 处的切线斜率为3.
处的切线斜率为3.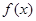 的解析式;
的解析式;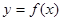 在[-4,1]上的最大值和最小值
在[-4,1]上的最大值和最小值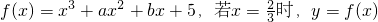 有极值,且曲线y=f(x)在点f(1)处的切线斜率为3.
有极值,且曲线y=f(x)在点f(1)处的切线斜率为3.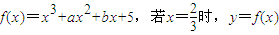 有极值,且曲线y=f(x)在点f(1)处的切线斜率为3.
有极值,且曲线y=f(x)在点f(1)处的切线斜率为3.