题目内容
已知函数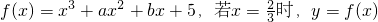 有极值,且曲线y=f(x)在点f(1)处的切线斜率为3.
有极值,且曲线y=f(x)在点f(1)处的切线斜率为3.
(1)求函数f(x)的解析式;
(2)求y=f(x)在[-4,1]上的最大值和最小值.
解:(1)f'(x)=3x2+2ax+b.
由题意,得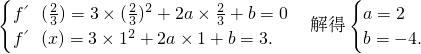
所以,f(x)=x3+2x2-4x+5.
(2)由(1)知f'(x)=x3+4x-4=(x+2)(3x-2).
 .
.
∴f(x)在[-4,1]上的最大值为13,最小值为-11.
分析:(1)先求函数f(x)=x3+ax2+bx+5的导函数,再由x= 时,y=f(x)有极值,列一方程,曲线y=f(x)在点f(1)处的切线斜率为3,列一方程,联立两方程即可得a、b值
时,y=f(x)有极值,列一方程,曲线y=f(x)在点f(1)处的切线斜率为3,列一方程,联立两方程即可得a、b值
(2)先求函数f(x)=x3+ax2+bx+5的导函数,再解不等式得函数的单调区间,最后列表列出端点值f(-4),f(1)及极值,通过比较求出y=f(x)在[-4,1]上的最大值和最小值
点评:本题考查了导数在函数极值和函数最值中的应用,解题时要耐心细致,规范解题步骤,避免出错.
由题意,得
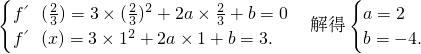
所以,f(x)=x3+2x2-4x+5.
(2)由(1)知f'(x)=x3+4x-4=(x+2)(3x-2).
 .
.| x | -4 | (-4,-2) | -2 | 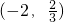 |  |  | 1 |
| f(x) | + | 0 | - | 0 | + | ||
| f(x) | 极大值 | 极小值 | |||||
| 函数值 | -11 | 13 |  | 4 |
分析:(1)先求函数f(x)=x3+ax2+bx+5的导函数,再由x=
 时,y=f(x)有极值,列一方程,曲线y=f(x)在点f(1)处的切线斜率为3,列一方程,联立两方程即可得a、b值
时,y=f(x)有极值,列一方程,曲线y=f(x)在点f(1)处的切线斜率为3,列一方程,联立两方程即可得a、b值(2)先求函数f(x)=x3+ax2+bx+5的导函数,再解不等式得函数的单调区间,最后列表列出端点值f(-4),f(1)及极值,通过比较求出y=f(x)在[-4,1]上的最大值和最小值
点评:本题考查了导数在函数极值和函数最值中的应用,解题时要耐心细致,规范解题步骤,避免出错.

练习册系列答案
相关题目
 有极值,且曲线y=f(x)在点f(1)处的切线斜率为3.
有极值,且曲线y=f(x)在点f(1)处的切线斜率为3.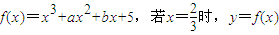 有极值,且曲线y=f(x)在点f(1)处的切线斜率为3.
有极值,且曲线y=f(x)在点f(1)处的切线斜率为3.