题目内容

P是双曲线
x2
a2
-
y2
b2
=1（a＞0，b＞0）右支上一点，F1、F2分别是左、右焦点，且焦距为2c，则△PF1F2的内切圆圆心的横坐标为
 
．
分析：根据题意，利用切线长定理，再利用双曲线的定义，把|PF1|-|PF2|=2a，转化为|HF1|-|HF2|=2a，从而求得点H的横坐标．
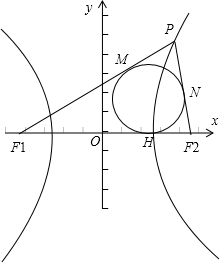
解答：解：如图所示：F1（-c，0）、F2（c，0），设内切圆与x轴的切点是点H，PF1、PF2分 与内切圆的切点分别为M、N，
∵由双曲线的定义可得|PF1|-|PF2|=2a，由圆的切线长定理知，|PM|=|PN|，故|MF1|-|NF2 |=2a，
即|HF1|-|HF2|=2a，设内切圆的圆心横坐标为x，则点H的横坐标为x，
故 （x+c）-（c-x）=2a，∴x=a．
故答案为：a．
精英家教网
点评：本题考查双曲线的定义、切线长定理，体现了转化的数学思想以及数形结合的数学思想．
练习册系列答案
相关题目
P是双曲线
x2
a2
-
y2
b2
=1(a＞0，b＞0)的右支上一点，F1，F2分别为双曲线的左、右焦点，焦距为2c，则△PF1F2的内切圆的圆心横坐标为（　　）
A、-aB、aC、-cD、c
已知P是双曲线
x2
a2
-
y2
b2
=1(a＞0，b＞0)的右支上一点，A1，A2分别为双曲线的左、右顶点，F1，F2分别为双曲线的左、右焦点，双曲线的离心率为e，有下列命题：
①双曲线的一条准线被它的两条渐近线所截得的线段长度为
2ab
a2+b2
；
②若|PF1|=e|PF2|，则e的最大值为
2
；
③△PF1F2的内切圆的圆心横坐标为a；
其中正确命题的序号是
 
．
设点P是双曲线
x2
a2
-
y2
b2
=1(a＞，b＞0)与圆x2+y2=a2+b2在第一象限的交点，F1、F2分别是双曲线的左、右焦点，且|PF1|=3|PF2|，则双曲线的离心率（　　）
已知A，B，P是双曲线
x2
a2
-
y2
b2
=1上不同的三点，且A，B连线经过坐标原点，若直线PA，PB的斜率乘积kPA•kPB=
2
3
，则该双曲线的离心率为
15
3
15
3
．
椭圆与双曲线之间有许多类似的性质：
P是椭圆
x2
a2
+
y2
b2
=1（a＞b＞0）上任一点，焦点F1、F2，∠F1PF2=α，三角形PF1F2面积为b2
sinα
1+cosα
，类比，P是双曲线
x2
a2
-
y2
b2
=1（a＞0，b＞0）上任一点，焦点F1、F2，∠F1PF2=α，三角形PF1F2面积为
b2
sinα
1-cosα
b2
sinα
1-cosα
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网