题目内容
设S是满足下列两个条件的实数所构成的集合:①1∉S;②若a∈S,则
∈S.试解答下列问题:
(1)若2∈S,则S中必还有其他两个元素,求出这两个元素;
(2)求证:若a∈S,则1-
∈S;
(3)在集合S中,元素的个数能否只有1个?请说明理由.
| 1 |
| 1-a |
(1)若2∈S,则S中必还有其他两个元素,求出这两个元素;
(2)求证:若a∈S,则1-
| 1 |
| a |
(3)在集合S中,元素的个数能否只有1个?请说明理由.
(1)若2∈S,则
=-1∈S,则
=
∈S,所以
=2∈S,此时元素循环,
所以S中必还有其他两个元素,这两个元素为-1和
.
(2)若a∈S,
∈S,则
=1-
∈S,所以(2)成立.
(3)不能,若能的话则有
=a,即a2-a+1=0,此时判别式△=1-4=-3<0对应方程无解,所以a不存在.
| 1 |
| 1-2 |
| 1 |
| 1-(-1) |
| 1 |
| 2 |
| 1 | ||
1-
|
所以S中必还有其他两个元素,这两个元素为-1和
| 1 |
| 2 |
(2)若a∈S,
| 1 |
| 1-a |
| 1 | ||
1-
|
| 1 |
| a |
(3)不能,若能的话则有
| 1 |
| 1-a |

练习册系列答案
相关题目
 ,②若
,②若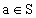 ,则
,则 ,求解下列问题:
,求解下列问题:
 中的项都在S中,求S中所含元素个数最少的集合
中的项都在S中,求S中所含元素个数最少的集合 ;
;
 中任取3个元素a,b,c,求使abc=-1的概率;
中任取3个元素a,b,c,求使abc=-1的概率;
 个吗?若是,请给出证明;若不是,试说明理由.
个吗?若是,请给出证明;若不是,试说明理由. ∈S.试解答下列问题:
∈S.试解答下列问题: ∈S;
∈S;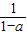 ∈S.试解答下列问题:
∈S.试解答下列问题: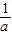 ∈S;
∈S;