题目内容
在△ABC中,4sinB•sin2(
+
)+cos2B=1+
.
(1)求角B的大小;(2)若a=4,cosC=sinB,求△ABC的面积.
| π |
| 4 |
| π |
| 2 |
| 3 |
(1)求角B的大小;(2)若a=4,cosC=sinB,求△ABC的面积.
分析:(1)把已知等式左边第一项的第二个因式利用二倍角的余弦函数公式化简,第二项也利用二倍角的余弦函数公式化简,去括号合并后,得出sinB的值,由B为三角形的内角,利用特殊角的三角函数值即可求出B的度数;
(2)由(1)求得的B的度数,得出sinB的值,进而由cosC=sinB得到cosC的值,可得出C的度数,若B=
时,得到此时三角形为直角三角形,由30度角所对的直角边等于斜边的一半可得出c与b的值,利用两直角边乘积的一半即可求出三角形ABC的面积;若B=
时,此时三角形为等腰三角形,作出底边AC上的高BD,根据30度角所对的直角边等于斜边的一半得出高BD的长,再根据勾股定理及三线合一性质得到AC的长,利用三角形的面积公式即可求出三角形ABC的面积.
(2)由(1)求得的B的度数,得出sinB的值,进而由cosC=sinB得到cosC的值,可得出C的度数,若B=
| π |
| 3 |
| 2π |
| 3 |
解答:解:(1)由4sinB•sin2(
+
)+cos2B=1+
得:
2sinB•[1-cos(
+B)]+1-2sin2B=1+
,
∴sinB=
,又∵B是△ABC的内角,
∴B=
或B=
;
(2)∵cosC=sinB,∴cosC=
,∴C=
,
若B=
时,则△ABC为直角三角形,又a=4,
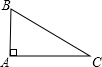
∴c=
a=2,b=2
,
∴S△ABC=
bc=2
;
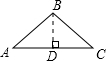
若B=
时,则△ABC为等腰三角形,又a=4,
过B作BD⊥AC,垂足为D,
∴BD=asin30°=2,
∴CD=2
,即AC=2DC=4
,
∴S△ABC=
AC•BD=4
.
综上所述:△ABC的面积为2
或4
.
| π |
| 4 |
| π |
| 2 |
| 3 |
2sinB•[1-cos(
| π |
| 2 |
| 3 |
∴sinB=
| 1 |
| 2 |
∴B=
| π |
| 3 |
| 2π |
| 3 |
(2)∵cosC=sinB,∴cosC=
| ||
| 2 |
| π |
| 6 |
若B=
| π |
| 3 |

∴c=
| 1 |
| 2 |
| 3 |
∴S△ABC=
| 1 |
| 2 |
| 3 |
若B=
| 2π |
| 3 |
过B作BD⊥AC,垂足为D,
∴BD=asin30°=2,
∴CD=2
| 3 |
| 3 |

∴S△ABC=
| 1 |
| 2 |
| 3 |
综上所述:△ABC的面积为2
| 3 |
| 3 |
点评:此题考查了二倍角的余弦函数公式,以及特殊角的三角函数值,利用了转化及数形结合的数学思想,根据B的度数有两解,可得三角形形状有两种,学生做题时要借助图形来求解,注意不要漏解.

练习册系列答案
 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
 +
+ )+cos2B=1+
)+cos2B=1+ .
.