题目内容
在△ABC中,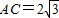 ,点B是椭圆
,点B是椭圆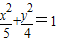 的上顶点,l是双曲线x2-y2=-2位于x轴下方的准线,当AC在直线l上运动时.
的上顶点,l是双曲线x2-y2=-2位于x轴下方的准线,当AC在直线l上运动时.(1)求△ABC外接圆的圆心P的轨迹E的方程;
(2)过定点F(0,
 )作互相垂直的直线l1、l2,分别交轨迹E于点M、N和点R、Q.求四边形MRNQ的面积的最小值.
)作互相垂直的直线l1、l2,分别交轨迹E于点M、N和点R、Q.求四边形MRNQ的面积的最小值.
【答案】分析:(1)先求出B点坐标以及直线l的方程,再根据△ABC外接圆的圆心时三边垂直平分线的交点,也即AC,AB垂直平分线,再利用垂直平分线的性质,用消参法求出P的轨迹E的方程.
(2)先设直线l1、l2,其中一条的方程.因为两直线互相垂直,所以另一条直线方程也可知,在分别于轨迹E的方程联立,求|MN|,|RQ|,再带着参数求四边形MRNQ的面积,用均值不等式求最小值.
解答:解:(1)由椭圆方程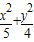 =1及双曲线方程x2-y2=-2可得点B(0,2),直线l的方程是y=-1.
=1及双曲线方程x2-y2=-2可得点B(0,2),直线l的方程是y=-1.
∵AC=2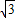 ,且AC在直线l上运动.
,且AC在直线l上运动.
可设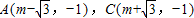 ,则AC的垂直平分线方程为x=m①
,则AC的垂直平分线方程为x=m①
AB的垂直平分线方程为y-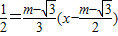 ②
②
∵P是△ABC的外接圆圆心,∴点P的坐标(x,y)满足方程①和②.
由①和②联立消去m得:y=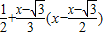 ,即y=
,即y=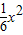 .
.
故圆心P的轨迹E的方程为x2=6y
(2)如图,直线l1和l2的斜率存在且不为零,设l1的方程为y=kx+
∵l1⊥l2,∴l2的方程为y=-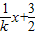
由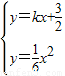 得x2-6kx-9=0∵△=36k2+36>0,∴直线l1与轨迹E交于两点.
得x2-6kx-9=0∵△=36k2+36>0,∴直线l1与轨迹E交于两点.
设M(x1,y1),N(x2,y2),则x1+x2=6k,x1x2=-9
∴|MN|=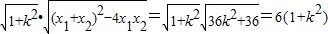
同理可得: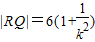
∴四边形MRNQ的面积S= |MN|•|QF|+
|MN|•|QF|+ |MN|•|RF|=
|MN|•|RF|= |MN|(|QF|+|RF|)=
|MN|(|QF|+|RF|)=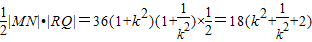 ≥
≥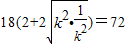
当且仅当k2=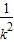 ,即k=±1时,等号成立.故四边形MRNQ的面积的最小值为72.
,即k=±1时,等号成立.故四边形MRNQ的面积的最小值为72.
点评:本题考查了消参法求轨迹方程,以及圆锥曲线与均值不等式联系求最值.
(2)先设直线l1、l2,其中一条的方程.因为两直线互相垂直,所以另一条直线方程也可知,在分别于轨迹E的方程联立,求|MN|,|RQ|,再带着参数求四边形MRNQ的面积,用均值不等式求最小值.
解答:解:(1)由椭圆方程
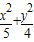 =1及双曲线方程x2-y2=-2可得点B(0,2),直线l的方程是y=-1.
=1及双曲线方程x2-y2=-2可得点B(0,2),直线l的方程是y=-1.∵AC=2
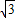 ,且AC在直线l上运动.
,且AC在直线l上运动.可设
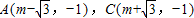 ,则AC的垂直平分线方程为x=m①
,则AC的垂直平分线方程为x=m①AB的垂直平分线方程为y-
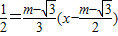 ②
②∵P是△ABC的外接圆圆心,∴点P的坐标(x,y)满足方程①和②.
由①和②联立消去m得:y=
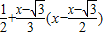 ,即y=
,即y=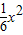 .
.故圆心P的轨迹E的方程为x2=6y
(2)如图,直线l1和l2的斜率存在且不为零,设l1的方程为y=kx+

∵l1⊥l2,∴l2的方程为y=-
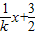
由
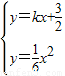 得x2-6kx-9=0∵△=36k2+36>0,∴直线l1与轨迹E交于两点.
得x2-6kx-9=0∵△=36k2+36>0,∴直线l1与轨迹E交于两点.设M(x1,y1),N(x2,y2),则x1+x2=6k,x1x2=-9
∴|MN|=
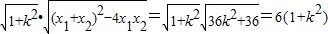
同理可得:
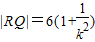
∴四边形MRNQ的面积S=
 |MN|•|QF|+
|MN|•|QF|+ |MN|•|RF|=
|MN|•|RF|= |MN|(|QF|+|RF|)=
|MN|(|QF|+|RF|)=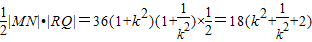 ≥
≥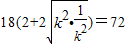
当且仅当k2=
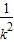 ,即k=±1时,等号成立.故四边形MRNQ的面积的最小值为72.
,即k=±1时,等号成立.故四边形MRNQ的面积的最小值为72.点评:本题考查了消参法求轨迹方程,以及圆锥曲线与均值不等式联系求最值.

练习册系列答案
相关题目
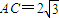 ,点B是椭圆
,点B是椭圆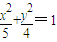 的上顶点,l是双曲线x2-y2=-2位于x轴下方的准线,当AC在直线l上运动时.
的上顶点,l是双曲线x2-y2=-2位于x轴下方的准线,当AC在直线l上运动时. )作互相垂直的直线l1、l2,分别交轨迹E于点M、N和点R、Q.求四边形MRNQ的面积的最小值.
)作互相垂直的直线l1、l2,分别交轨迹E于点M、N和点R、Q.求四边形MRNQ的面积的最小值.