题目内容
【题目】如图所示,在四棱台![]() 中,
中, ![]() 底面
底面![]() ,四边形
,四边形![]() 为菱形,
为菱形, ![]() ,
, ![]() .
.
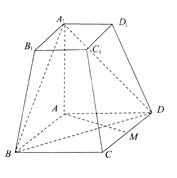
(Ⅰ)若![]() 为
为![]() 中点,求证:
中点,求证: ![]() 平面
平面![]() ;
;
(Ⅱ)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)详见解析;(2)![]() .
.
【解析】(Ⅰ)要证直线![]() 与平面
与平面![]() 垂直,现在由
垂直,现在由![]() 与底面垂直有
与底面垂直有![]() ,因此还要证一个垂直,证
,因此还要证一个垂直,证![]() ,这可通过等边三角形
,这可通过等边三角形![]() 得证
得证![]() ,从而有需要的结论
,从而有需要的结论![]() ,因此证得线面垂直;
,因此证得线面垂直;
(Ⅱ)要求直线与平面所成的角,分别以![]() 为
为![]() 轴、
轴、![]() 轴、
轴、![]() 轴,建立如图所示的空间直角坐标系
轴,建立如图所示的空间直角坐标系![]() ,
, ![]() 、
、![]() 、
、![]() 、
、 ,求出平面
,求出平面![]() 的法向量,由直线的方向向量与平面法向量夹角得线面角.
的法向量,由直线的方向向量与平面法向量夹角得线面角.
试题解析:(Ⅰ) ![]() 四边形为菱形,
四边形为菱形, ![]() ,连结
,连结![]() ,则
,则![]() 为等边三角形,
为等边三角形,
又![]() 为
为![]() 中点,
中点, ![]() ,由
,由![]() 得,
得, ![]() ,
,
![]() 底面
底面![]() ,
, ![]() 底面
底面![]() ,
, ![]() ,又
,又![]() ,
,
![]() 平面
平面![]()
(Ⅱ)![]() 四边形
四边形![]() 为菱形,
为菱形, ![]() ,
, ![]() ,
,
得![]() ,
, ![]() ,
, ![]() ,又
,又![]() 底面
底面![]() ,
,
分别以![]() 为
为![]() 轴、
轴、![]() 轴、
轴、![]() 轴,建立如图所示的空间直角坐标系
轴,建立如图所示的空间直角坐标系![]() ,
,
![]() 、
、![]() 、
、![]() 、
、 ,
,
 ,
, ![]() ,
, ![]() ,
,
设平面![]() 的一个法向量
的一个法向量![]() ,
,
则有 ,令
,令![]() ,则
,则![]()
![]() 直线
直线![]() 与平面
与平面![]() 所成角
所成角![]() 的正弦值
的正弦值
 .
.


练习册系列答案
相关题目
【题目】如果从不包括大小王的52张扑克牌中随机抽取一张,那么取到红心(事件A)的概率是![]() ,取到方块(事件B)的概率是
,取到方块(事件B)的概率是![]() ,问:
,问:
(1)取到红色牌(事件C)的概率是多少?
(2)取到黑色牌(事件D)的概率是多少?