题目内容
抛物线方程为y2=p(x+1)(p>0),直线x+y=m与x轴的交点在抛物线的准线的右边.
(1)求证:直线与抛物线总有两个交点;
(2)设直线与抛物线的交点为Q、R,OQ⊥OR,
求p关于m的函数f(m)的表达式;
(3)在(2)的条件下,若抛物线焦点F到直线x+y=m的距离为
,
求此直线的方程.
(1)求证:直线与抛物线总有两个交点;
(2)设直线与抛物线的交点为Q、R,OQ⊥OR,
求p关于m的函数f(m)的表达式;
(3)在(2)的条件下,若抛物线焦点F到直线x+y=m的距离为
| ||
| 2 |
求此直线的方程.
(1)抛物线y2=p(x+1)的准线方程是x=-1-
,
直线x+y=m与x轴的交点为(m,0),
题设交点在准线右边,
得m>-1-
,即4m+p+4>0.
由
,
得x2-(2m+p)x+(m2-p)=0.
而判别式△=(2m+p)2-4(m2-p)=p(4m+p+4).
又p>0及4m+p+4>0,
可知△>0.
因此,直线与抛物线总有两个交点; …(4分)
(2)设Q、R两点的坐标分别为(x1,y1)、(x2,y2),
由(1)知,x1、x2是方程x2-(2m+p)x+m2-p=0的两根,
∴x1+x2=2m+p,x1•x2=m2-p.
由OQ⊥OR,得kOQ•kOR=-1,
即有x1x2+y1y2=0.
又Q、R为直线x+y=m上的点,
因而y1=-x1+m,y2=-x2+m.
于是x1x2+y1y2=2x1x2-m(x1+x2)+m2=2(m2-p)-m(2m+p)+m2=0,
∴p=f(m)=
,
由
,
得m>-2,m≠0;…(9分)
(3)由于抛物线y2=p(x+1)的焦点F坐标为(-1+
,0),
于是有
=
,
即|p-4m-4|=4.
又p=
,
∴|
|=4.
解得m1=0,m2=-
,m3=-4,m4=-
.
但m≠0且m>-2,因而舍去m1、m2、m3,
故所求直线方程为3x+3y+4=0.…(14分)
| p |
| 4 |
直线x+y=m与x轴的交点为(m,0),
题设交点在准线右边,
得m>-1-
| p |
| 4 |
由
|
得x2-(2m+p)x+(m2-p)=0.
而判别式△=(2m+p)2-4(m2-p)=p(4m+p+4).
又p>0及4m+p+4>0,
可知△>0.
因此,直线与抛物线总有两个交点; …(4分)
(2)设Q、R两点的坐标分别为(x1,y1)、(x2,y2),
由(1)知,x1、x2是方程x2-(2m+p)x+m2-p=0的两根,
∴x1+x2=2m+p,x1•x2=m2-p.
由OQ⊥OR,得kOQ•kOR=-1,
即有x1x2+y1y2=0.
又Q、R为直线x+y=m上的点,
因而y1=-x1+m,y2=-x2+m.
于是x1x2+y1y2=2x1x2-m(x1+x2)+m2=2(m2-p)-m(2m+p)+m2=0,
∴p=f(m)=
| m2 |
| m+2 |
由
|
得m>-2,m≠0;…(9分)
(3)由于抛物线y2=p(x+1)的焦点F坐标为(-1+
| p |
| 4 |
于是有
|-1+
| ||
|
| ||
| 2 |
即|p-4m-4|=4.
又p=
| m2 |
| m+2 |
∴|
| 3m2+12m+8 |
| m+2 |
解得m1=0,m2=-
| 8 |
| 3 |
| 4 |
| 3 |
但m≠0且m>-2,因而舍去m1、m2、m3,
故所求直线方程为3x+3y+4=0.…(14分)

练习册系列答案
相关题目
 ,求p的值的范围.
,求p的值的范围. ,求p的值的范围.
,求p的值的范围.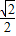 ,
,