题目内容
抛物线方程为y2=p(x+1)(p>0),直线x+y=m与x轴的交点在抛物线的准线的右边.
(1)求证:直线与抛物线总有两个交点;
(2)设直线与抛物线的交点为Q、R,OQ⊥OR,求p关于m的函数f(m)的表达式;
(3)在(2)的条件下,若m变化,使得原点O到直线QR的距离不大于
,求p的值的范围.
(1)求证:直线与抛物线总有两个交点;
(2)设直线与抛物线的交点为Q、R,OQ⊥OR,求p关于m的函数f(m)的表达式;
(3)在(2)的条件下,若m变化,使得原点O到直线QR的距离不大于
| ||
| 2 |
分析:(1)由抛物线的性质可得抛物线的准线方程x=-1-
,由直线x+y=m与x轴的交点为(m,0)在准线右边可得,m>-1-
,要证直线与抛物线总有两个交点,只要证明由
所得方程x2-(2m+p)x+(m2-p)=0的判别式△>0即可
(2)设Q、R两点的坐标分别为(x1,y1)、(x2,y2),由(1)知,x1、x2是方程x2-(2m+p)x+m2-p=0的两根,由方程的根与系数的关系及由OQ⊥OR,可得x1x2+y1y2=0可求
(3)解法一:由题意可得
≤
可求m的范围,结合(2)中m>-2且m≠0可求m的范围,而f(m)=
=(m+2)+
-4,利用函数单调性的定义可求p的范围
解法二:由解法一可知,m的范围,由(2)知p=f(m)=
=
,利用二次函数的单调性可求p的范围
| p |
| 4 |
| p |
| 4 |
|
(2)设Q、R两点的坐标分别为(x1,y1)、(x2,y2),由(1)知,x1、x2是方程x2-(2m+p)x+m2-p=0的两根,由方程的根与系数的关系及由OQ⊥OR,可得x1x2+y1y2=0可求
(3)解法一:由题意可得
| |0+0-m| | ||
|
| ||
| 2 |
| m2 |
| m+2 |
| 4 |
| m+2 |
解法二:由解法一可知,m的范围,由(2)知p=f(m)=
| m2 |
| m+2 |
| 1 | ||||
|
解答:解:(1)∵抛物线y2=p(x+1)的准线方程是x=-1-
∵直线x+y=m与x轴的交点为(m,0)在准线右边
∴m>-1-
∴m>-1-
,即4m+p+4>0.
由
得x2-(2m+p)x+(m2-p)=0.
而判别式△=(2m+p)2-4(m2-p)=p(4m+p+4).
又p>0及4m+p+4>0,可知△>0.
因此,直线与抛物线总有两个交点; …(4分)
(2)设Q、R两点的坐标分别为(x1,y1)、(x2,y2),
由(1)知,x1、x2是方程x2-(2m+p)x+m2-p=0的两根,
∴x1+x2=2m+p,x1•x2=m2-p.由OQ⊥OR,得kOQ•kOR=-1,
即有x1x2+y1y2=0.又Q、R为直线x+y=m上的点,
因而y1=-x1+m,y2=-x2+m.
于是x1x2+y1y2=2x1x2-m(x1+x2)+m2=2(m2-p)-m(2m+p)+m2=0,
∴p=f(m)=
,由
得m>-2,m≠0;…(9分)
(3)解法一:由于原点O到直线x+y=m的距离不大于
,于是
≤
,
∴|m|≤1.由(2),知m>-2且m≠0
故m∈[-1,0)∪(0,1].
由(2),知f(m)=
=(m+2)+
-4qqqq1q
当m∈[-1,0)时,任取m1、m2,0>m1>m2≥-1,则
f(m1)-f(m2)=(m1-m2)+(
-
)
=(m1-m2)[1-
].
由0>m1>m2≥-1,知0<(m1+2)(m2+2)<4,1-
<0.
又由m1-m2>0知f(m1)<f(m2)因而f(m)为减函数.
可见,当m∈[-1,0)时,p∈(0,1].
同样可证,当m∈(0,1]时,f(m)为增函数,从而p∈(0,
].
解法二:由解法一知,m∈[-1,0)∪(0,1].由(2)知
p=f(m)=
=
.
设t=
,g(t)=t+2t2,则t∈(-∞,-1]∪[1,+∞),
又g(t)=2t2+t=2(t+
)2-
.
∴当t∈(-∞,-1]时,g(t)为减函数,g(t)∈[1,+∞).
当t∈[1,+∞)时,g(t)为增函数,g(t)∈[3,+∞).
因此,当m∈[-1,0]时,t∈(-∞,-1],p=
∈(0,1];
当m∈(0,1]时,t∈[1,+∞),p∈(0,
].
| p |
| 4 |
∵直线x+y=m与x轴的交点为(m,0)在准线右边
∴m>-1-
| p |
| 4 |
∴m>-1-
| p |
| 4 |
由
|
得x2-(2m+p)x+(m2-p)=0.
而判别式△=(2m+p)2-4(m2-p)=p(4m+p+4).
又p>0及4m+p+4>0,可知△>0.
因此,直线与抛物线总有两个交点; …(4分)
(2)设Q、R两点的坐标分别为(x1,y1)、(x2,y2),
由(1)知,x1、x2是方程x2-(2m+p)x+m2-p=0的两根,
∴x1+x2=2m+p,x1•x2=m2-p.由OQ⊥OR,得kOQ•kOR=-1,
即有x1x2+y1y2=0.又Q、R为直线x+y=m上的点,
因而y1=-x1+m,y2=-x2+m.
于是x1x2+y1y2=2x1x2-m(x1+x2)+m2=2(m2-p)-m(2m+p)+m2=0,
∴p=f(m)=
| m2 |
| m+2 |
|
(3)解法一:由于原点O到直线x+y=m的距离不大于
| ||
| 2 |
| |0+0-m| | ||
|
| ||
| 2 |
∴|m|≤1.由(2),知m>-2且m≠0
故m∈[-1,0)∪(0,1].
由(2),知f(m)=
| m2 |
| m+2 |
| 4 |
| m+2 |
当m∈[-1,0)时,任取m1、m2,0>m1>m2≥-1,则
f(m1)-f(m2)=(m1-m2)+(
| 4 |
| m1+2 |
| 4 |
| m2+2 |
=(m1-m2)[1-
| 4 |
| (m1+2)(m2+2) |
由0>m1>m2≥-1,知0<(m1+2)(m2+2)<4,1-
| 4 |
| (m1+2)(m2+2) |
又由m1-m2>0知f(m1)<f(m2)因而f(m)为减函数.
可见,当m∈[-1,0)时,p∈(0,1].
同样可证,当m∈(0,1]时,f(m)为增函数,从而p∈(0,
| 1 |
| 3 |
解法二:由解法一知,m∈[-1,0)∪(0,1].由(2)知
p=f(m)=
| m2 |
| m+2 |
| 1 | ||||
|
设t=
| 1 |
| m |
又g(t)=2t2+t=2(t+
| 1 |
| 4 |
| 1 |
| 8 |
∴当t∈(-∞,-1]时,g(t)为减函数,g(t)∈[1,+∞).
当t∈[1,+∞)时,g(t)为增函数,g(t)∈[3,+∞).
因此,当m∈[-1,0]时,t∈(-∞,-1],p=
| 1 |
| g(t) |
当m∈(0,1]时,t∈[1,+∞),p∈(0,
| 1 |
| 3 |
点评:本题主要考查了抛物线的性质的应用,直线与抛物线的相交关系与系数的应用,及利用函数的单调性求解函数的取值范围,属于方程与函数知识的综合应用.

练习册系列答案
相关题目
 ,求p的值的范围.
,求p的值的范围. ,求p的值的范围.
,求p的值的范围.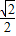 ,
,