题目内容
设函数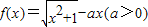 ,
,(I)求证:当且仅当a≥1时,f(x)在[0,+∞)内为单调函数;
(II)求a的取值范围,使函数f(x)在区间[1,+∞)上是增函数.
【答案】分析:(I)先求函数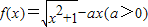 的导数f′(x),再证明a≥1时,f′(x)<0,f(x)单调;而a<1时,f′(x)先负后正,f(x)不单调
的导数f′(x),再证明a≥1时,f′(x)<0,f(x)单调;而a<1时,f′(x)先负后正,f(x)不单调
(II)由(1)知a≥1时f(x)单调递减,不合题意,当0<a<1时,使函数f(x)在区间[1,+∞)上是增函数,需[1,+∞)是函数单调增区间的子区间,可求a的范围
解答:解:(I)∵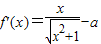 ,
,
①当a≥1时,∵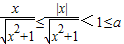 ,∴f(x)在[0,+∞)上单调递减
,∴f(x)在[0,+∞)上单调递减
②当0<a<1时,由f′(x)<0,得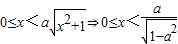 ;
;
由f′(x)>0得 ;
;
∴当0<a<1时,f(x)在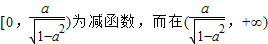 ,为增函数,
,为增函数,
∴当0<a<1时,f(x)在[0,+∞)上不是单调函数;
综上,当且仅当a≥1时,f(x)在[0,+∞)上为单调函数.
(II)由(I)①知当a≥1时f(x)单调递减,不合; 由②知当f(x)在[1,+∞)上单调递增等价于: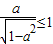 ,∴
,∴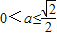 ,即a的取值范围是
,即a的取值范围是 .
.
点评:本题考查了导数在函数的单调性上的应用,解题时要学会对参数进行讨论,做到不重不漏,还要注意一题中两问间的关系
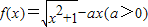 的导数f′(x),再证明a≥1时,f′(x)<0,f(x)单调;而a<1时,f′(x)先负后正,f(x)不单调
的导数f′(x),再证明a≥1时,f′(x)<0,f(x)单调;而a<1时,f′(x)先负后正,f(x)不单调(II)由(1)知a≥1时f(x)单调递减,不合题意,当0<a<1时,使函数f(x)在区间[1,+∞)上是增函数,需[1,+∞)是函数单调增区间的子区间,可求a的范围
解答:解:(I)∵
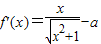 ,
,①当a≥1时,∵
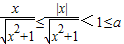 ,∴f(x)在[0,+∞)上单调递减
,∴f(x)在[0,+∞)上单调递减②当0<a<1时,由f′(x)<0,得
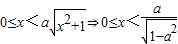 ;
;由f′(x)>0得
 ;
;∴当0<a<1时,f(x)在
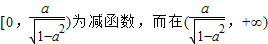 ,为增函数,
,为增函数,∴当0<a<1时,f(x)在[0,+∞)上不是单调函数;
综上,当且仅当a≥1时,f(x)在[0,+∞)上为单调函数.
(II)由(I)①知当a≥1时f(x)单调递减,不合; 由②知当f(x)在[1,+∞)上单调递增等价于:
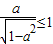 ,∴
,∴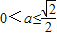 ,即a的取值范围是
,即a的取值范围是 .
.点评:本题考查了导数在函数的单调性上的应用,解题时要学会对参数进行讨论,做到不重不漏,还要注意一题中两问间的关系

练习册系列答案
相关题目
 ,若存在开区间
,若存在开区间 和常数C,使得对任意的
和常数C,使得对任意的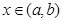 都有
都有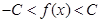 ,且对任意的x
,且对任意的x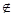 (a,b)都有
(a,b)都有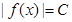 恒成立,则称函数
恒成立,则称函数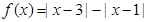 是R上的“Z型”函数;
是R上的“Z型”函数; 对任意的x
对任意的x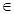 R恒成立,求实数t的取值范围.
R恒成立,求实数t的取值范围.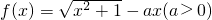 ,
,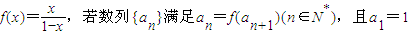 .
.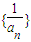 是等差数列;
是等差数列;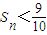 成立的n的最大值.
成立的n的最大值.