题目内容
已知某种同型号的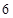
瓶饮料中有
瓶已过了保质期.
（1）从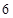瓶饮料中任意抽取
瓶，求抽到没过保质期的饮料的概率；
（2）从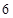瓶饮料中随机抽取瓶，求抽到已过保质期的饮料的概率.
（1）
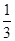；（2）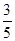
.
解析试题分析：将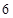瓶饮料根据是否过保质期分为两类，分别进行编号，以示区别，然后利用列举法并结合古典概型的概率计算公式计算（1）和（2）中两个事件的概率.
试题解析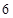：瓶饮料中未过保质期的有
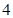瓶，将这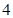瓶分别记为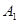
、
、
、
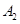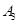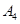，瓶过保质期的饮料分别记为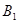
、
.
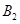（1）记事件
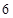：从瓶饮料中任意抽取瓶，抽到没过保质期的饮料，
则抽到没过保质期的饮料所包含的基本事件分别为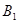、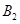，共两个，而基本事件的总数为，
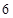由古典概型的概率计算公式得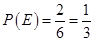
，即抽到没过保质期的饮料的概率为；
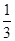（2）记事件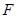
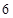：从瓶饮料中随机抽取瓶，抽到已过保质期的饮料，
基本事件有：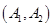
、
、
、
、
、
、
、
、
、
、
、
、
、
、
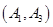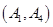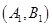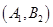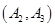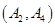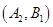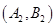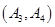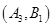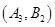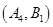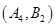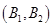，共
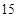个，
其中事件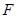所包含的基本事件有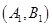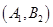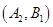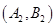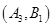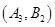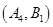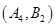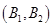：、、、、、、、、，共
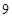个，
由古典概型的概率计算公式得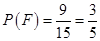
，即抽到已过保质期的饮料的概率为.
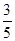考点：1.古典概型；2.列举法
练习册系列答案
赢在课堂名师课时计划系列答案
相关题目
为了提高食品的安全度,某食品安检部门调查了一个海水养殖场的养殖鱼的有关情况,安检人员从这个海水养殖场中不同位置共捕捞出100条鱼,称得每条鱼的质量(单位:kg),并将所得数据进行统计得下表.若规定超过正常生长速度(1.0～1.2 kg/年)的比例超过15%,则认为所饲养的鱼有问题,否则认为所饲养的鱼没有问题.
| 鱼的 质量 | [1.00, 1.05) | [1.05, 1.10) | [1.10, 1.15) | [1.15, 1.20) | [1.20, 1.25) | [1.25, 1.30) |
| 鱼的 条数 | 3 | 20 | 35 | 31 | 9 | 2 |
(2)上面捕捞的100条鱼中间,从质量在[1.00,1.05)和[1.25,1.30)的鱼中,任取2条鱼来检测,求恰好所取得的鱼的质量在[1.00,1.05)和[1.25,1.30)各有1条的概率.
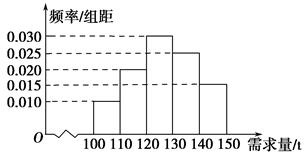
名网友的网购金额情况，得到如下数据统计表（如图）：
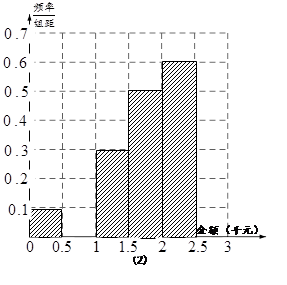
千元的顾客定义为“网购达人”，网购金额不超过
．
，
，
，
的值，并补全频率分布直方图（如图(2)）．
名网友的购物体验，从“非网购达人”、“网购达人”中用分层抽样的方法确定
人，若需从这
人进行问卷调查．设
为选取的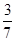
，
.
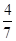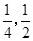；两小时以上且不超过三小时还车的概率分别为
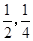；两人租车时间都不会超过四小时.
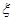，求
.
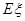V”的事件为X，求概率P(X)；