题目内容
【题目】已知![]() 的三边长分别为
的三边长分别为![]() ,
,![]() ,
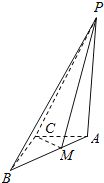
,![]() ,M是AB边上的点,P是平面ABC外一点.给出下列四个命题:①若
,M是AB边上的点,P是平面ABC外一点.给出下列四个命题:①若![]() 平面ABC,则三棱锥
平面ABC,则三棱锥![]() 的四个面都是直角三角形;②若
的四个面都是直角三角形;②若![]() 平面ABC,且M是边AB的中点,则有
平面ABC,且M是边AB的中点,则有![]() ;③若
;③若![]() ,
,![]() 平面ABC,则
平面ABC,则![]() 面积的最小值为
面积的最小值为![]() ;④若
;④若![]() ,P在平面ABC上的射影是
,P在平面ABC上的射影是![]() 内切圆的圆心,则点P到平面ABC的距离为
内切圆的圆心,则点P到平面ABC的距离为![]() .其中正确命题的序号是________.(把你认为正确命题的序号都填上)
.其中正确命题的序号是________.(把你认为正确命题的序号都填上)
【答案】①②④
【解析】
①:利用勾股定理及逆定理和线面垂直的判定定理和性质定理可以判断本命题的真假;
②:根据直角三角形斜边的性质和勾股定理可以判断出本命题的真假;
③:利用面积公式和勾股定理可以判断出本命题的真假;
④:利用直角三角形内切圆的性质以及勾股定理可以判断出本命题的真假;
因为![]() ,
,![]() ,
,![]() ,所以
,所以![]() ,即
,即![]()
①:由上可知: ![]() 是直角三角形.
是直角三角形. ![]() 平面ABC,而
平面ABC,而![]() 平面ABC,因此
平面ABC,因此
![]() ,所以
,所以![]() 是直角三角形.因为
是直角三角形.因为
![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,而
,而
![]() 平面
平面![]() ,所以
,所以![]() ,因此
,因此![]() 是直角三角形,故本命题是真命题;
是直角三角形,故本命题是真命题;
②:因为![]() 是以
是以![]() 为斜边的直角三角形, M是边AB的中点,所以
为斜边的直角三角形, M是边AB的中点,所以![]() ,
,
又![]() 平面ABC,
平面ABC, ![]() 平面ABC,所以
平面ABC,所以![]() ,由勾股定理可知:
,由勾股定理可知:
![]() ,而
,而![]() ,
,
所以![]() ,故本命题是真命题;
,故本命题是真命题;
③:![]() ,当
,当![]() 最小时,
最小时,![]() 面积有最小值,所以当
面积有最小值,所以当
![]() 时,此时
时,此时![]() ,所以
,所以![]() 面积最小值为6,故本命题是假命题;
面积最小值为6,故本命题是假命题;
④:由内切圆关径公式可知:内切圆的半径![]() ,故
,故![]() ,设P在平面ABC上的射影是
,设P在平面ABC上的射影是![]() 内切圆的圆心为O,因此有
内切圆的圆心为O,因此有![]() ,
,
所以![]() ,所以点P到平面ABC的距离为
,所以点P到平面ABC的距离为![]() .故本命题是真命题;
.故本命题是真命题;
故答案为:①②④

练习册系列答案
相关题目





