题目内容
设某物体一天中的温度T是时间t的函数,已知T(t)=at3+bt2+ct+d(a≠0),其中温度的单位是℃,时间的单位是小时,中午12:00相应的t=0,中午12:00以后相应的t取正数,中午12:00以前相应的t取负数(如早上8:00相应的t=-4,下午16:00相应的t=4),若测得该物体在早上8:00的温度为8℃,中午12:00的温度为60℃,下午13:00的温度为58℃,且已知该物体的温度在早上8:00与下午16:00有相同的变化率.
(1)求该物体的温度T关于时间t的函数关系式;
(2)该物体在上午10:00至下午14:00这段时间中(包括端点)何时温度最高?最高温度是多少?
(1)求该物体的温度T关于时间t的函数关系式;
(2)该物体在上午10:00至下午14:00这段时间中(包括端点)何时温度最高?最高温度是多少?
分析:(1)求导函数,利用该物体的温度在早上8:00与下午16:00有相同的变化率,建立方程,求得b的值,再利用该物体在早上8:00的温度为8℃,中午12:00的温度为60℃,下午13:00的温度为58℃,建立方程组,即可确定函数的解析式;
(2)确定函数在[-2,2]上的单调性,从而可得函数的极值与最值,即可求得结论.
(2)确定函数在[-2,2]上的单调性,从而可得函数的极值与最值,即可求得结论.
解答:解:(1)求导函数可得T′=3at2+2bt+c
∵该物体的温度在早上8:00与下午16:00有相同的变化率
∴T′(-4)=T′(4),∴12a-8b+c=12a+8b+c,∴b=0
∵该物体在早上8:00的温度为8℃,中午12:00的温度为60℃,下午13:00的温度为58℃
∴
∴a=1,b=0,c=-3,d=60
∴T(t)=t3-3t2+60(-12≤t≤12);
(2)T′=3t2-3=3(t+1)(t-1),
令T′>0,可得t<-1或t>1;令T′<0,可得-1<t<1
∴函数在(-2,-1)上单调递增,在(-1,1)上单调递减,在(1,2)上单调递增
∵T(-2)=58,T(-1)=62,T(1)=58,T(2)=62
∴t=-1或t=2时,T(t)取到最大值62,说明在上午11:00与下午14:00,该物体温度最高,最高温度是62℃.
∵该物体的温度在早上8:00与下午16:00有相同的变化率
∴T′(-4)=T′(4),∴12a-8b+c=12a+8b+c,∴b=0
∵该物体在早上8:00的温度为8℃,中午12:00的温度为60℃,下午13:00的温度为58℃
∴
|
∴a=1,b=0,c=-3,d=60
∴T(t)=t3-3t2+60(-12≤t≤12);
(2)T′=3t2-3=3(t+1)(t-1),
令T′>0,可得t<-1或t>1;令T′<0,可得-1<t<1
∴函数在(-2,-1)上单调递增,在(-1,1)上单调递减,在(1,2)上单调递增
∵T(-2)=58,T(-1)=62,T(1)=58,T(2)=62
∴t=-1或t=2时,T(t)取到最大值62,说明在上午11:00与下午14:00,该物体温度最高,最高温度是62℃.
点评:本题考查利用数学知识解决实际问题,考查函数解析式的确定,考查导数知识的运用,考查计算能力,属于中档题.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
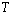 是时间
是时间 的函数,已知
的函数,已知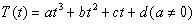 ,其中温度的单位是℃,时间的单位是小时.中午12:00相应的
,其中温度的单位是℃,时间的单位是小时.中午12:00相应的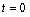 ,中午12:00以后相应的
,中午12:00以后相应的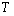 是时间
是时间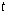 的函数,已知
的函数,已知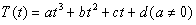 ,其中温度的单位是℃,时间的单位是小时.中午12:00相应的
,其中温度的单位是℃,时间的单位是小时.中午12:00相应的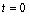 ,中午12:00以后相应的
,中午12:00以后相应的