Question

(理)如图a所示，在平面直角坐标系中，O为坐标原点，M为动点，且,= .过点M作MM₁⊥y轴于M₁，过N作NN₁⊥x轴于点N₁．又动点T满足=+ ，其轨迹为曲线C．

(1)求曲线C的方程；

(2)已知点A(5，0)、B(1，0)，过点A作直线交曲线C于两个不同的点P、Q，△BPQ的面积S是否存在最大值?若存在，求出其最大值；若不存在，请说明理由．

(文)如图b所示，线段AB过x轴正半轴上一点M(m，0)(m＞0)，端点A，B到x轴距离之积为2m，以x轴为对称轴、过A，O，B三点作抛物线．

(1)求抛物线方程；

(2)若tan∠AOB=-1，求m的取值范围．

第21题图

Answer 1

答案：(理)(1)设点T的坐标为(x，y)，点M的坐标为(x′，y′)，则M₁的坐标为(0，y′)．

∵,

∴点N的坐标为.

∴N₁的坐标为(),

∴=(x′,0),

∵，∴,

又∵，∴x′²+y′²=5．

∴x²+=5，即=1为曲线C的方程．

(2)点A(5，0)在曲线C即椭圆的外部，当直线l的斜率不存在时，直线l与椭圆C无交点，所以直线l的斜率存在．又三点B、P、Q可构成三角形，

∴设直线l的方程为：x-my=5(m0)．

由方程组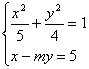，得(4m²+5)y²+40my+80=0.

依题意△=320(m²-5)＞0，得m＞或m＜.

设点P(x₁，y₁)，Q(x₂，y₂)．

点B到直线l的距离为d=

|PQ|=|y₁-y₂|=.

∴S_△BPQ=d·|PQ|

=

即S_△BPQ=.

下面考查函数t=.

∵

=16(m²-5)+200≥400，

当且仅当16(m²-5)=即m=±时等号成立，满足条件m＞或m＜.

此时m＜t²≤，0＜t≤，0＜S_△BPQ≤.

∴△BPQ的面积S存在最大值为.

(文)(1)当AB不垂直于x轴时，设AB方程为y=k(x-m)，抛物线方程为y²=2px(p＞0)

由得ky²-2py-2pkm=0，

∴y₁y₂=-2pm，∴|y₁y₂|=2pm=2m

∴p=1．

当AB⊥x轴时，A，B分别为(m，)，(m，)，由题意有2pm=2m，P=1，故所求抛物线方程为y²=2x．

(2)设A(，y₁)，B(，y₂)

由(1)知y₁y₂=-2m，y₁+y₂=.

∴|y₁-y₂|=,

又tan∠AOB=-1，k₁=，k₂=，

∴,

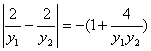即y₁y₂+4=2|y₁-y₂|，

∴-2m+4=                                                        ①

平方后化简得m²-12m+4=

∴m²-12m+4＞0，∴m＜6或m＞6+

又由①知-2m+4＞0，∴m＜2，

∴m的取值范围为0＜m＜6

当m=6且AB⊥x轴时，y₁=2(-1)，y₂=-2(-1)，y₁y₂=-4(-1)²=-2m．

tan∠AOB=-1符合条件，故符合条件的m的取值范围为0＜m≤6.